Advertisements
Advertisements
Question
Construct a parallelogram ABCD such that l(BC) = 7 cm, m∠ABC = 40° , l(AB) = 3 cm.
Solution
Steps of Construction:
Step 1: Draw AB = 3 cm.
Step 2: Draw ∠ABX = 40°
Step 3: With B as the center and radius 7 cm, draw an arc cutting the ray BX at C.
Step 4: With C as centre and radius 3 cm, draw an arc.
Step 5: With A as the center and a radius of 7 cm, draw an arc cutting the previous arc at D.
Step 6: Join AD and CD.

Here, ABCD is the required parallelogram.
RELATED QUESTIONS
Consider the given parallelogram. Find the values of the unknowns x, y, z.
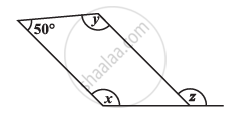
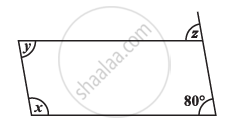
Consider the given parallelograms. Find the values of the unknowns x, y, z.
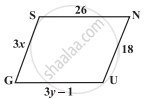
The following figure GUNS is a parallelogram. Find x and y. (Lengths are in cm)
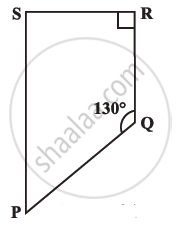
Find the measure of ∠P and ∠S, if `bar(SP) || bar(RQ)` in the following figure. (If you find m∠R, is there more than one method to find m∠P?).
Perimeter of a parallelogram is 150 cm. One of its sides is greater than the other side by 25 cm. Find the lengths of all sides.
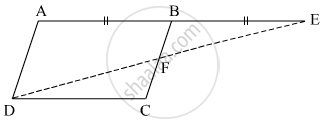
In the given figure, `square`ABCD is a parallelogram. Point E is on the ray AB such that BE = AB then prove that line ED bisects seg BC at point F.
Given: Parallelogram ABCD in which diagonals AC and BD intersect at M.
Prove: M is the mid-point of LN.
In the following diagram, the bisectors of interior angles of the parallelogram PQRS enclose a quadrilateral ABCD.
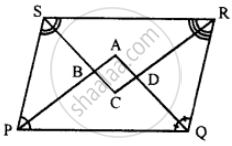
Show that:
(i) ∠PSB + ∠SPB = 90°
(ii) ∠PBS = 90°
(iii) ∠ABC = 90°
(iv) ∠ADC = 90°
(v) ∠A = 90°
(vi) ABCD is a rectangle
Thus, the bisectors of the angles of a parallelogram enclose a rectangle.
The given figure shows parallelogram ABCD. Points M and N lie in diagonal BD such that DM = BN.
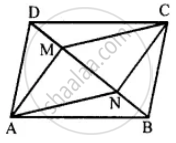
Prove that:
(i) ∆DMC = ∆BNA and so CM = AN
(ii) ∆AMD = ∆CNB and so AM CN
(iii) ANCM is a parallelogram.
ABCD is a parallelogram. The bisector of angle A intersects CD at X and bisector of angle C intersects AB at Y. Is AXCY a parallelogram? Give reason.
