Advertisements
Advertisements
Question
Referring the adjacent figure of a parallelogram, write the answer of questions given below.
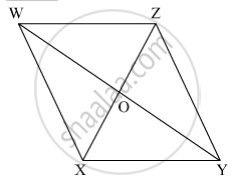
(1) If l(WZ) = 4.5 cm then l(XY) = ?
(2) If l(YZ) = 8.2 cm then l(XW) = ?
(3) If l(OX) = 2.5 cm then l(OZ) = ?
(4) If l(WO) = 3.3 cm then l(WY) = ?
(5) If m∠WZY = 120° then m∠WXY = ? and m∠XWZ = ?
Solution
WXYZ is a parallelogram.
(1) l(XY) = l(WZ) = 4.5 cm ...(Opposite sides of a parallelogram are congruent)
(2) l(XW) = l(YZ) = 8.2 cm ...(Opposite sides of a parallelogram are congruent)
(3) l(OZ) = l(OX) = 2.5 cm ...(Diagonals of parallelogram bisect each other)
(4) l(WY) = 2 × l(WO) = 2 × 3.3 = 6.6 cm ...(Diagonals of parallelogram bisect each other)
(5) m∠WXY = m∠WZY = 120º ...(Opposite angles of a parallelogram are congruent)
Now,
m∠WZY + m∠XWZ = 180º ...(Adjacent angles of a parallelogram are supplementary)
⇒ 120º + m∠XWZ = 180º
⇒ m∠XWZ = 180º − 120º = 60º
RELATED QUESTIONS
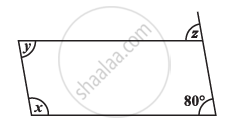
Consider the given parallelograms. Find the values of the unknowns x, y, z.
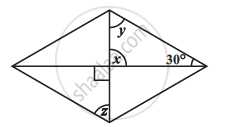
Consider the given parallelograms. Find the values of the unknowns x, y, z.
The measures of two adjacent angles of a parallelogram are in the ratio 3 : 2. Find the measure of each of the angles of the parallelogram.
Construct ☐ BARC such that l(BA) = l(BC) = 4.2 cm, l(AC) = 6.0 cm, l(AR) = l(CR) = 5.6 cm
In parallelogram PQRS, ∠Q = (4x – 5)° and ∠S = (3x + 10)°. Calculate: ∠Q and ∠R.
In the following diagram, the bisectors of interior angles of the parallelogram PQRS enclose a quadrilateral ABCD.
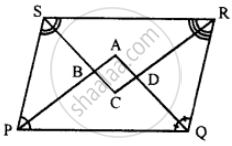
Show that:
(i) ∠PSB + ∠SPB = 90°
(ii) ∠PBS = 90°
(iii) ∠ABC = 90°
(iv) ∠ADC = 90°
(v) ∠A = 90°
(vi) ABCD is a rectangle
Thus, the bisectors of the angles of a parallelogram enclose a rectangle.
In the given figure, ABCD and BDCE are parallelograms with common base DC. If BC ⊥ BD, then ∠BEC = ______.

In parallelogram MODE, the bisector of ∠M and ∠O meet at Q, find the measure of ∠MQO.
ABCD is a parallelogram. Find the value of x, y and z.

Construct a parallelogram when one of its side is 4 cm and its two diagonals are 5.6 cm and 7 cm. Measure the other side.
