Advertisements
Advertisements
Question
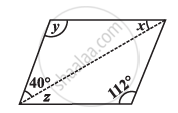
ABCD is a parallelogram. Find the value of x, y and z.

Solution
Given, A parallelogram ABCD.
In the ΔOBC, we have
y + 30° = 100° ...[Exterior angle property of triangle]
⇒ y = 70°
By the angle sum property of a triangle,
We have, x + y + 30° = 180°
⇒ x + 70° + 30° = 180°
⇒ x = 180° – 100°
⇒ x = 80°
Now, since AD || BC and BD is transversal,
Therefore, ∠ADO = ∠OBC ...[Alternative interior angles]
⇒ z = 30°
APPEARS IN
RELATED QUESTIONS
Given a parallelogram ABCD. Complete each statement along with the definition or property used.
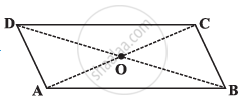
- AD = ______
- ∠DCB = ______
- OC = ______
- m∠DAB + m∠CDA = ______
Consider the given parallelograms. Find the values of the unknowns x, y, z.
Can a quadrilateral ABCD be a parallelogram if ∠A = 70° and ∠C = 65°?
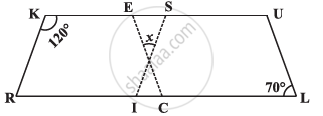
In the above figure both RISK and CLUE are parallelograms. Find the value of x.
In the given figure, G is the point of concurrence of medians of ΔDEF. Take point H on ray DG such that D-G-H and DG = GH, then prove that `square`GEHF is a parallelogram.

Construct ☐ BARC such that l(BA) = l(BC) = 4.2 cm, l(AC) = 6.0 cm, l(AR) = l(CR) = 5.6 cm
In parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.
In the following diagram, the bisectors of interior angles of the parallelogram PQRS enclose a quadrilateral ABCD.
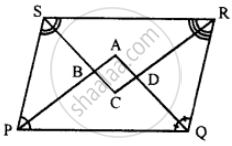
Show that:
(i) ∠PSB + ∠SPB = 90°
(ii) ∠PBS = 90°
(iii) ∠ABC = 90°
(iv) ∠ADC = 90°
(v) ∠A = 90°
(vi) ABCD is a rectangle
Thus, the bisectors of the angles of a parallelogram enclose a rectangle.
In the given figure, AB || EC, AB = AC and AE bisects ∠DAC. Prove that:
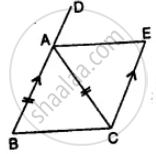
- ∠EAC = ∠ACB
- ABCE is a parallelogram.
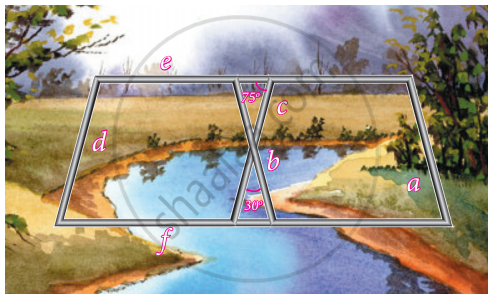
Iron rods a, b, c, d, e, and f are making a design in a bridge as shown in the figure. If a || b, c || d, e || f, find the marked angles between d and e