Advertisements
Advertisements
प्रश्न
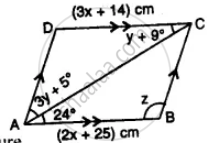
ABCD is a parallelogram. Find the value of x, y and z.

उत्तर
Given, A parallelogram ABCD.
In the ΔOBC, we have
y + 30° = 100° ...[Exterior angle property of triangle]
⇒ y = 70°
By the angle sum property of a triangle,
We have, x + y + 30° = 180°
⇒ x + 70° + 30° = 180°
⇒ x = 180° – 100°
⇒ x = 80°
Now, since AD || BC and BD is transversal,
Therefore, ∠ADO = ∠OBC ...[Alternative interior angles]
⇒ z = 30°
APPEARS IN
संबंधित प्रश्न
Given a parallelogram ABCD. Complete each statement along with the definition or property used.
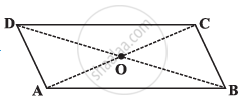
- AD = ______
- ∠DCB = ______
- OC = ______
- m∠DAB + m∠CDA = ______
The measures of two adjacent angles of a parallelogram are in the ratio 3 : 2. Find the measure of each of the angles of the parallelogram.
Name the quadrilaterals whose diagonals bisect each other
In parallelogram ABCD, E is the mid-point of side AB and CE bisects angle BCD. Prove that :
(i) AE = AD,
(ii) DE bisects and ∠ADC and
(iii) Angle DEC is a right angle.
In the following diagram, the bisectors of interior angles of the parallelogram PQRS enclose a quadrilateral ABCD.
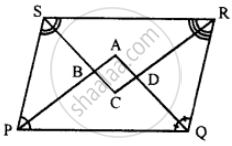
Show that:
(i) ∠PSB + ∠SPB = 90°
(ii) ∠PBS = 90°
(iii) ∠ABC = 90°
(iv) ∠ADC = 90°
(v) ∠A = 90°
(vi) ABCD is a rectangle
Thus, the bisectors of the angles of a parallelogram enclose a rectangle.
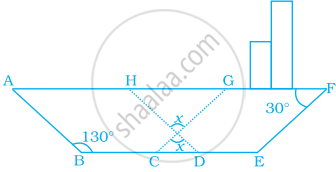
Use the information given in the alongside diagram to find the value of x, y, and z.
In the given figure, ABCD and BDCE are parallelograms with common base DC. If BC ⊥ BD, then ∠BEC = ______.

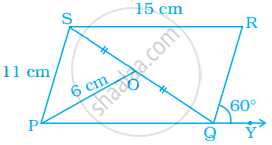
In parallelogram PQRS, O is the mid point of SQ. Find ∠S, ∠R, PQ, QR and diagonal PR.
In the following figure of a ship, ABDH and CEFG are two parallelograms. Find the value of x.
The angle between the two altitudes of a parallelogram through the vertex of an obtuse angle of the parallelogram is 45°. Find the angles of the parallelogram.
