Advertisements
Advertisements
प्रश्न
In a quadrilateral HOPE, PS and ES are bisectors of ∠P and ∠E respectively. Give reason.
उत्तर
Given, HOPE is a quadrilateral.
PS and ES are bisectors of ∠P and ∠E respectively.
A quadrilateral is a closed shape that is formed by joining four points among which any three points are non-collinear.
A quadrilateral is a closed shape and a type of polygon that has four sides, four vertices and four angles.
The sum of interior angles of quadrilaterals is always equal to 360 degrees.
The diagonals of the quadrilateral bisect each other.
The diagonals divide the quadrilateral into two pairs of congruent triangles.
The intersection point of the diagonals is also the intersection point of the lines connecting the midpoints of the opposite sides of the quadrilateral.
Therefore, the data is insufficient.
APPEARS IN
संबंधित प्रश्न
All squares are trapeziums.
In `square`ABCD, side BC || side AD, side AB ≅ side DC If ∠A = 72° then find the measure of ∠B and ∠D.
In an Isosceles-trapezium, show that the opposite angles are supplementary.
Which of the following figures satisfy the following property?
- Only one pair of sides are parallel.
Which of the following properties describe a trapezium?
A quadrilateral in which a pair of opposite sides is parallel is ______.
Every rhombus is a trapezium.
Of the four quadrilaterals-square, rectangle, rhombus and trapezium-one is somewhat different from the others because of its design. Find it and give justification.
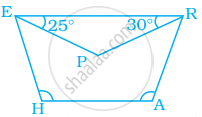
In trapezium HARE, EP and RP are bisectors of ∠E and ∠R respectively. Find ∠HAR and ∠EHA.
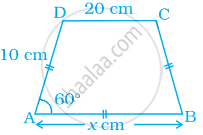
In the following figure, AB || DC and AD = BC. Find the value of x.