Advertisements
Advertisements
प्रश्न
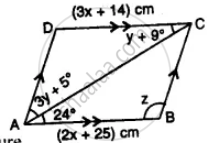
Use the information given in the alongside diagram to find the value of x, y, and z.
उत्तर
ABCD is a parallelogram and AC is its diagonal which bisects the opposite angle
Opposite sides of a parallelogram are equal
3x + 14 = 2x + 25
⇒ 3x – 2x = 25 – 14
⇒ x = 11
∴ x = 11 cm
∠DCA = ∠CAB (Alternate angles)
y + 9° = 24
y = 24° – 9° = 15°
∠DAB = 3y° + 5° + 24° = 3 x 15 + 5 + 24° = 50° + 24° = 74°
∠ABC =180°- ∠DAB = 180° – 74° = 106°
z = 106°
Hence x = 11 cm, y = 15°, z = 106°
APPEARS IN
संबंधित प्रश्न
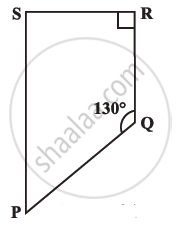
Find the measure of ∠P and ∠S, if `bar(SP) || bar(RQ)` in the following figure. (If you find m∠R, is there more than one method to find m∠P?).
Name the quadrilaterals whose diagonals bisect each other
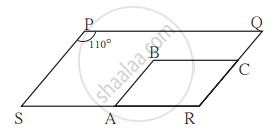
In the given figure, `square`PQRS and `square`ABCR are two parallelograms. If ∠P = 110° then find the measures of all angles of `square`ABCR.
ABCD is a parallelogram. What kind of quadrilateral is it if : AC = BD and AC is perpendicular to BD?
If a triangle and a parallelogram lie on the same base and between the same parallels, then prove that the area of the triangle is equal to half of the area of parallelogram
All rectangles are parallelograms.
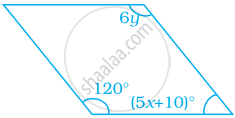
Find the values of x and y in the following parallelogram.
Two angles of a quadrilateral are each of measure 75° and the other two angles are equal. What is the measure of these two angles? Name the possible figures so formed.
In parallelogram ABCD, the angle bisector of ∠A bisects BC. Will angle bisector of B also bisect AD? Give reason.
Construct a parallelogram when one of its side is 4 cm and its two diagonals are 5.6 cm and 7 cm. Measure the other side.
