Advertisements
Advertisements
Question
Use the information given in the alongside diagram to find the value of x, y, and z.
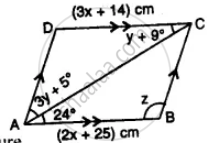
Solution
ABCD is a parallelogram and AC is its diagonal which bisects the opposite angle
Opposite sides of a parallelogram are equal
3x + 14 = 2x + 25
⇒ 3x – 2x = 25 – 14
⇒ x = 11
∴ x = 11 cm
∠DCA = ∠CAB (Alternate angles)
y + 9° = 24
y = 24° – 9° = 15°
∠DAB = 3y° + 5° + 24° = 3 x 15 + 5 + 24° = 50° + 24° = 74°
∠ABC =180°- ∠DAB = 180° – 74° = 106°
z = 106°
Hence x = 11 cm, y = 15°, z = 106°
APPEARS IN
RELATED QUESTIONS
Can a quadrilateral ABCD be a parallelogram if AB = DC = 8 cm, AD = 4 cm and BC = 4.4 cm?
Can a quadrilateral ABCD be a parallelogram if ∠A = 70° and ∠C = 65°?
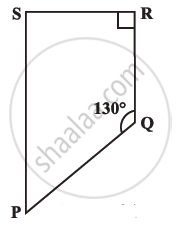
Find the measure of ∠P and ∠S, if `bar(SP) || bar(RQ)` in the following figure. (If you find m∠R, is there more than one method to find m∠P?).
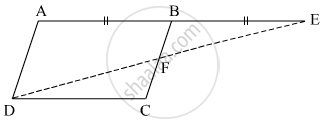
In the given figure, `square`ABCD is a parallelogram. Point E is on the ray AB such that BE = AB then prove that line ED bisects seg BC at point F.
Construct ☐ BARC such that l(BA) = l(BC) = 4.2 cm, l(AC) = 6.0 cm, l(AR) = l(CR) = 5.6 cm
If opposite angles of a quadrilateral are equal, it must be a parallelogram.
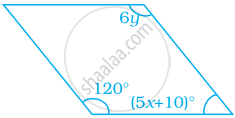
Find the values of x and y in the following parallelogram.
A diagonal of a parallelogram bisects an angle. Will it also bisect the other angle? Give reason.
Construct a parallelogram ABCD in which AB = 4 cm, BC = 5 cm and ∠B = 60°.
Draw a rough figure of a quadrilateral that is not a parallelogram but has exactly two opposite angles of equal measure.
