Advertisements
Advertisements
Question
Construct ☐ BARC such that l(BA) = l(BC) = 4.2 cm, l(AC) = 6.0 cm, l(AR) = l(CR) = 5.6 cm
Solution
Steps of Construction:
Step 1: Draw BA = 4.2 cm.
Step 2: With B as the centre and a radius of 4.2 cm, draw an arc.
Step 3: With A as the centre and a radius of 6 cm, draw an arc cutting the previous arc at C.
Step 4: Join BC.
Step 5: With A as the centre and a radius of 5.6 cm, draw an arc.
Step 6: With C as the centre and a radius of 5.6 cm, draw an arc cutting the previous arc at R.
Step 7: Join AR and CR.
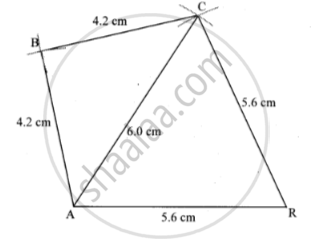
Here, BARC is the required quadrilateral.
RELATED QUESTIONS
The measures of two adjacent angles of a parallelogram are in the ratio 3 : 2. Find the measure of each of the angles of the parallelogram.
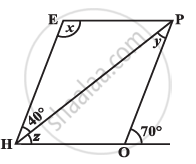
The adjacent figure HOPE is a parallelogram. Find the angle measures x, y and z. State the properties you use to find them.
In parallelogram PQRS, ∠Q = (4x – 5)° and ∠S = (3x + 10)°. Calculate: ∠Q and ∠R.
PQRS is a parallelogram whose diagonals intersect at M.
If ∠PMS = 54°, ∠QSR = 25° and ∠SQR = 30° ; find :
(i) ∠RPS
(ii) ∠PRS
(iii) ∠PSR.
In the given figure, AB || EC, AB = AC and AE bisects ∠DAC. Prove that:
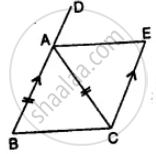
- ∠EAC = ∠ACB
- ABCE is a parallelogram.
Which of the following figures satisfy the following properties?
- All sides are congruent.
- All angles are right angles.
- Opposite sides are parallel.
If two adjacent angles of a parallelogram are (5x – 5)° and (10x + 35)°, then the ratio of these angles is ______.
In the given figure, ABCD and BDCE are parallelograms with common base DC. If BC ⊥ BD, then ∠BEC = ______.

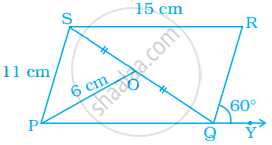
In parallelogram PQRS, O is the mid point of SQ. Find ∠S, ∠R, PQ, QR and diagonal PR.
Two angles of a quadrilateral are each of measure 75° and the other two angles are equal. What is the measure of these two angles? Name the possible figures so formed.
