Advertisements
Advertisements
Question
PQRS is a parallelogram whose diagonals intersect at M.
If ∠PMS = 54°, ∠QSR = 25° and ∠SQR = 30° ; find :
(i) ∠RPS
(ii) ∠PRS
(iii) ∠PSR.
Solution
Given : ||gm PQRS in which diagonals PR & QS intersect at M.
∠PMS = 54° ; ∠QSR = 25° and ∠SQR=30°
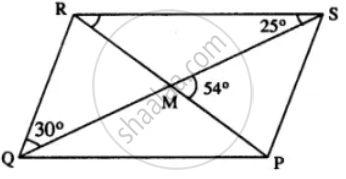
To find : (i) ∠RPS (ii) ∠PRS (iii) ∠PSR
Proof : QR || PS
⇒ ∠PSQ = ∠SQR (Alternate ∠s)
But ∠SQR = 30° (Given)
∠PSQ = 30°
In ∆SMP,
∠PMS + ∠ PSM +∠MPS = 180° or 54° + 30° + ∠RPS
= 180°
∠RPS = 180°- 84° = 96°
Now ∠PRS + ∠RSQ = ∠PMS
∠PRS + 25° =54°
∠PRS = 54° – 25° = 29°
∠PSR = ∠PSQ + ∠RSQ = 30°+25° = 55°
Hence (i) ∠RPS = 96° (ii) ∠PRS = 29° (iii) ∠PSR = 55°
APPEARS IN
RELATED QUESTIONS
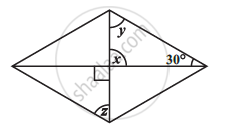
Consider the given parallelograms. Find the values of the unknowns x, y, z.
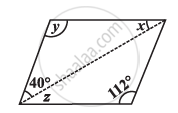
Consider the given parallelograms. Find the values of the unknowns x, y, z.
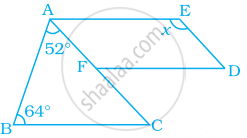
Can a quadrilateral ABCD be a parallelogram if AB = DC = 8 cm, AD = 4 cm and BC = 4.4 cm?
Ratio of consecutive angles of a quadrilateral is 1 : 2 : 3 : 4. Find the measure of its each angle. Write, with reason, what type of a quadrilateral it is.
Construct a parallelogram ABCD such that l(BC) = 7 cm, m∠ABC = 40° , l(AB) = 3 cm.
In parallelogram ABCD, X and Y are midpoints of opposite sides AB and DC respectively. Prove that:
(i) AX = YC
(ii) AX is parallel to YC
(iii) AXCY is a parallelogram.
In the given figure, AB || EC, AB = AC and AE bisects ∠DAC. Prove that:
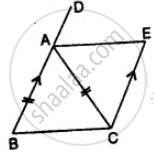
- ∠EAC = ∠ACB
- ABCE is a parallelogram.
If two adjacent angles of a parallelogram are (5x – 5)° and (10x + 35)°, then the ratio of these angles is ______.
In parallelogram PQRS, O is the mid point of SQ. Find ∠S, ∠R, PQ, QR and diagonal PR.
In the following figure, FD || BC || AE and AC || ED. Find the value of x.