Advertisements
Advertisements
प्रश्न
PQRS is a parallelogram whose diagonals intersect at M.
If ∠PMS = 54°, ∠QSR = 25° and ∠SQR = 30° ; find :
(i) ∠RPS
(ii) ∠PRS
(iii) ∠PSR.
उत्तर
Given : ||gm PQRS in which diagonals PR & QS intersect at M.
∠PMS = 54° ; ∠QSR = 25° and ∠SQR=30°
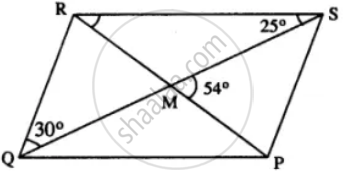
To find : (i) ∠RPS (ii) ∠PRS (iii) ∠PSR
Proof : QR || PS
⇒ ∠PSQ = ∠SQR (Alternate ∠s)
But ∠SQR = 30° (Given)
∠PSQ = 30°
In ∆SMP,
∠PMS + ∠ PSM +∠MPS = 180° or 54° + 30° + ∠RPS
= 180°
∠RPS = 180°- 84° = 96°
Now ∠PRS + ∠RSQ = ∠PMS
∠PRS + 25° =54°
∠PRS = 54° – 25° = 29°
∠PSR = ∠PSQ + ∠RSQ = 30°+25° = 55°
Hence (i) ∠RPS = 96° (ii) ∠PRS = 29° (iii) ∠PSR = 55°
APPEARS IN
संबंधित प्रश्न
Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.
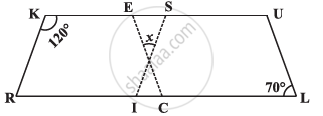
In the above figure both RISK and CLUE are parallelograms. Find the value of x.
In the given figure, if points P, Q, R, S are on the sides of parallelogram such that AP = BQ = CR = DS then prove that `square`PQRS is a parallelogram.

Ratio of two adjacent sides of a parallelogram is 3 : 4, and its perimeter is 112 cm. Find the length of its each side.
ABCD is a parallelogram. What kind of quadrilateral is it if: AC is perpendicular to BD but is not equal to it?
In the given figure, AB || EC, AB = AC and AE bisects ∠DAC. Prove that:
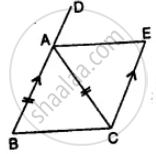
- ∠EAC = ∠ACB
- ABCE is a parallelogram.
The angle between the two altitudes of a parallelogram through the same vertex of an obtuse angle of the parallelogram is 30°. The measure of the obtuse angle is ______.
Two angles of a quadrilateral are each of measure 75° and the other two angles are equal. What is the measure of these two angles? Name the possible figures so formed.
The angle between the two altitudes of a parallelogram through the vertex of an obtuse angle of the parallelogram is 45°. Find the angles of the parallelogram.
ABCD is a parallelogram. Points P and Q are taken on the sides AB and AD respectively and the parallelogram PRQA is formed. If ∠C = 45°, find ∠R.
