Advertisements
Advertisements
प्रश्न
The angle between the two altitudes of a parallelogram through the same vertex of an obtuse angle of the parallelogram is 30°. The measure of the obtuse angle is ______.
विकल्प
100°
150°
105°
120°
उत्तर
The angle between the two altitudes of a parallelogram through the same vertex of an obtuse angle of the parallelogram is 30°. The measure of the obtuse angle is 150°.
Explanation:
Let EC and FC be altitudes and ∠ECF = 30°.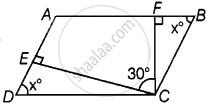
Let ∠EDC = x = ∠FBC
So, ∠ECD = 90° – x and ∠BCF = 90° – x
So, by property of the parallelogram,
∠ADC + ∠DCB = 180°
∠ADC + (∠ECD + ∠ECF + ∠BCF) = 180°
⇒ x + 90° – x + 30° + 90° – x = 180°
⇒ – x = 180° – 210° = – 30°
⇒ x = 30°
Hence, ∠DCB = 30° + 60° + 60° = 150°
APPEARS IN
संबंधित प्रश्न
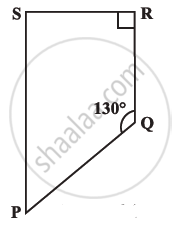
Find the measure of ∠P and ∠S, if `bar(SP) || bar(RQ)` in the following figure. (If you find m∠R, is there more than one method to find m∠P?).
Name the quadrilaterals whose diagonals bisect each other
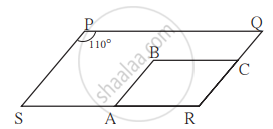
In the given figure, `square`PQRS and `square`ABCR are two parallelograms. If ∠P = 110° then find the measures of all angles of `square`ABCR.
Construct a parallelogram ABCD such that l(BC) = 7 cm, m∠ABC = 40° , l(AB) = 3 cm.
In parallelogram ABCD, X and Y are midpoints of opposite sides AB and DC respectively. Prove that:
(i) AX = YC
(ii) AX is parallel to YC
(iii) AXCY is a parallelogram.
The given figure shows parallelogram ABCD. Points M and N lie in diagonal BD such that DM = BN.
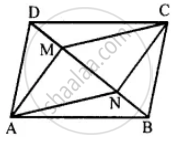
Prove that:
(i) ∆DMC = ∆BNA and so CM = AN
(ii) ∆AMD = ∆CNB and so AM CN
(iii) ANCM is a parallelogram.
All rectangles are parallelograms.
In parallelogram LOST, SN ⊥ OL and SM ⊥ LT. Find ∠STM, ∠SON and ∠NSM.

A diagonal of a parallelogram bisects an angle. Will it also bisect the other angle? Give reason.
Construct a parallelogram HOME with HO = 6 cm, HE = 4 cm and OE = 3 cm.
