Advertisements
Advertisements
प्रश्न
In parallelogram LOST, SN ⊥ OL and SM ⊥ LT. Find ∠STM, ∠SON and ∠NSM.

उत्तर
Given, ∠MST = 40°
In ΔMST,
By the angle sum property of a triangle,
∠TMS + ∠MST + ∠STM = 180°
⇒ ∠STM = 180° – (90° + 40°) ...[∵ SM ⊥ LT, ∠TMS = 90°]
= 50°
∴ ∠SON = ∠STM = 50° ...[∵ Opposite angles of a parallelogram are equal]
Now, In the ΔONS,
∠ONS + ∠OSN + ∠SON = 180° ...[Angle sum property of triangle]
∠OSN = 180° – (90° + 50°)
= 180° – 140°
= 40°
Moreover, ∠SON + ∠TSO = 180° ...[∵ Adjacent angles of a parallelogram are supplementary]
⇒ ∠SON + ∠TSM + ∠NSM + ∠OSN = 180°
⇒ 50° + 40° + ∠NSM + 40° = 180°
⇒ 90° + 40° + ∠NSM = 180°
⇒ 130° + ∠NSM = 180°
⇒ ∠NSM = 180° – 130° = 50°
APPEARS IN
संबंधित प्रश्न
Given a parallelogram ABCD. Complete each statement along with the definition or property used.
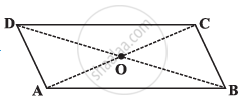
- AD = ______
- ∠DCB = ______
- OC = ______
- m∠DAB + m∠CDA = ______
The measures of two adjacent angles of a parallelogram are in the ratio 3 : 2. Find the measure of each of the angles of the parallelogram.
Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.
In the given figure, AB || EC, AB = AC and AE bisects ∠DAC. Prove that:
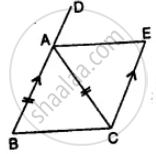
- ∠EAC = ∠ACB
- ABCE is a parallelogram.
If a triangle and a parallelogram lie on the same base and between the same parallels, then prove that the area of the triangle is equal to half of the area of parallelogram
In parallelogram PQRS, O is the mid point of SQ. Find ∠S, ∠R, PQ, QR and diagonal PR.
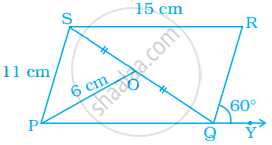
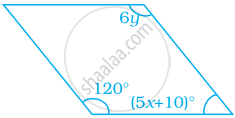
Find the values of x and y in the following parallelogram.
ABCD is a parallelogram. Points P and Q are taken on the sides AB and AD respectively and the parallelogram PRQA is formed. If ∠C = 45°, find ∠R.
In parallelogram ABCD, the angle bisector of ∠A bisects BC. Will angle bisector of B also bisect AD? Give reason.
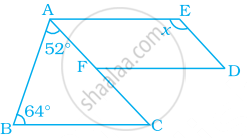
In the following figure, FD || BC || AE and AC || ED. Find the value of x.