Advertisements
Advertisements
प्रश्न
A rectangular MORE is shown below:
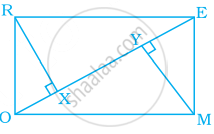
Answer the following questions by giving appropriate reason.
- Is RE = OM?
- Is ∠MYO = ∠RXE?
- Is ∠MOY = ∠REX?
- Is ΔMYO ≅ ΔRXE?
- Is MY = RX?
उत्तर
i. Yes, RE = OM
Given, MORE is a rectangle.
Therefore, opposite sides are equal.
ii. Yes, ∠MYO = ∠RXE
Here, MY and RX are perpendicular to OE.
Since, ∠RXO = 90°
⇒ ∠RXE = 90° and ∠MYE = 90°
⇒ ∠MYO = 90°
iii. Yes, ∠MOY = ∠REX
∵ RE || OM and EO is a transversal.
∴ ∠MOE = ∠OER ...[∵ Alternative interior angles]
⇒ ∠MOY = ∠REX
iv. Yes, ∆MYO ≅ ∆RXE
In ∆MYO and ∆RXE
MO = RE ...[Proved in (i)]
∠MOY = ∠REX ...[Proved in (iii)]
∠MYO = ∠RXE ...[Proved in (ii)]
∴ ∆MYO = ∆RXE ...[By AAS]
v. Yes, MY = RX
Since, these are corresponding parts of congruent triangles.
APPEARS IN
संबंधित प्रश्न
Which of the following statement true for a square?
Its diagonals are equal to its sides.
State with Reason Whether the Following Statement is ‘True’ Or ‘False’.
Every rectangle is a parallelogram.
Diagonals of a rectangle PQRS are intersecting in point M. If ∠QMR = 50° find the measure of ∠MPS.
The following figure is a rectangle in which x: y = 3: 7; find the values of x and y.
Show that the bisectors of angles of a parallelogram form a rectangle
A quadrilateral whose opposite sides and all the angles are equal is a ______.
If the diagonals of a quadrilateral are equal and bisect each other, then the quadrilateral is a ______.
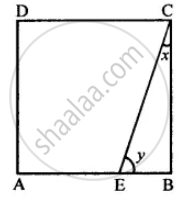
A playground is in the form of a rectangle ATEF. Two players are standing at the points F and B where EF = EB. Find the values of x and y.
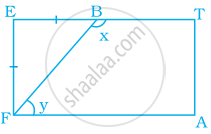
Quadrilateral EFGH is a rectangle in which J is the point of intersection of the diagonals. Find the value of x if JF = 8x + 4 and EG = 24x – 8.
A line l is parallel to line m and a transversal p intersects them at X, Y respectively. Bisectors of interior angles at X and Y interesct at P and Q. Is PXQY a rectangle? Given reason.
