Advertisements
Advertisements
प्रश्न
Diagonals of a rectangle PQRS are intersecting in point M. If ∠QMR = 50° find the measure of ∠MPS.
उत्तर
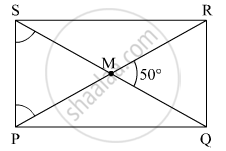
`square`PQRS is a rectangle.
∴ PM = `1/2` PR …(i)
MS = `1/2` QS …(ii) ...(Diagonals of a rectangle bisect each other)
Also, PR = QS …(iii) ...(Diagonals of a rectangle are congruent)
∴ PM = MS …(iv) ...[From (i), (ii) and (iii)]
In ∆PMS,
PM = MS ...[From (iv)]
∴ ∠MSP = ∠MPS = x° ...(v) ...(Isosceles triangle theorem)
∠PMS = ∠QMR = 50° ...(vi) ...(Vertically opposite angles)
In ∆MPS,
∠PMS + ∠MPS + ∠MSP = 180° ...(The sum of the measures of the three angles of a triangle is 180°.)
∴ 50° + x + x = 180° ...[From (v) and (vi)]
∴ 50° + 2x = 180°
∴ 2x = 180° - 50°
∴ 2x = 130°
∴ x = `(130°)/2`
∴ x = 65°
∴ ∠MPS = 65° ...[From (v)]
APPEARS IN
संबंधित प्रश्न
ABC is a right-angled triangle and O is the mid point of the side opposite to the right angle. Explain why O is equidistant from A, B and C. (The dotted lines are drawn additionally to help you)
In a parallelogram ABCD, the diagonals bisect each other at O. If ∠ABC = 30°, ∠BDC = 10° and ∠CAB = 70°. Find:
∠DAB, ∠ADC, ∠BCD, ∠AOD, ∠DOC, ∠BOC, ∠AOB, ∠ACD, ∠CAB, ∠ADB, ∠ACB, ∠DBC and ∠DBA.
Which of the following statement is true for a rectangle?
Its diagonals are equal and perpendicular, and bisect each other.
Which of the following statement true for a square?
Its diagonals are equal to its sides.
Fill in the blank in the following, so as to make the statement true:
A square is a rhombus in which .....
The sides of a rectangle are in the ratio 4 : 5. Find its sides if the perimeter is 90 cm.
Adjacent sides of a rectangle are 7 cm and 24 cm. Find the length of its diagonal.
If diagonal of a rectangle is 26 cm and one side is 24 cm, find the other side.
The interior angle made by the side in a parallelogram is 90° then the parallelogram is a
If the diagonals of a quadrilateral are equal and bisect each other, then the quadrilateral is a ______.
