Advertisements
Advertisements
प्रश्न
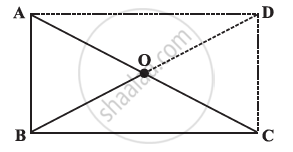
ABC is a right-angled triangle and O is the mid point of the side opposite to the right angle. Explain why O is equidistant from A, B and C. (The dotted lines are drawn additionally to help you)
उत्तर
ABCD is a rectangle as opposite sides are equal and parallel to each other, and all the interior angles are 90º.
In a rectangle, diagonals are of equal length and also these bisect each other.
Since MBC is right-angled at B. So ∠D = 90°, AD||BC and AB||DC
ABCD is a rectangle where AB = CD and AD=BC
AC and BD are the diagonals which bisect each other.
Hence, AO = OC = BO = OD
Thus, O is equidistant from A, B, and C.
APPEARS IN
संबंधित प्रश्न
In a parallelogram ABCD, the diagonals bisect each other at O. If ∠ABC = 30°, ∠BDC = 10° and ∠CAB = 70°. Find:
∠DAB, ∠ADC, ∠BCD, ∠AOD, ∠DOC, ∠BOC, ∠AOB, ∠ACD, ∠CAB, ∠ADB, ∠ACB, ∠DBC and ∠DBA.
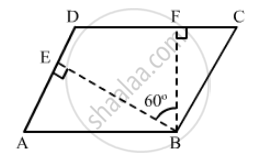
The angle between the altitudes of a parallelogram, through the same vertex of an obtuse angle of the parallelogram is 60°. Find the angles of the parallelogram.
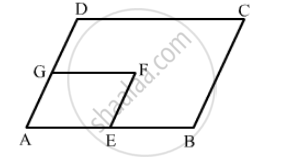
In the following figure, ABCD and AEFG are parallelograms. If ∠C = 55°, what is the measure of ∠F?
Which of the following statement is true for a rectangle?
Its diagonals are perpendicular and bisect each other.
A window frame has one diagonal longer than the other. Is the window frame a rectangle? Why or why not?
A mason has made a concrete slab. He needs it to be rectangular. In what different ways can he make sure that it is rectangular?
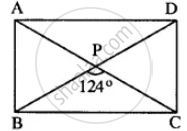
ABCD is a rectangle, if ∠BPC = 124°
Calculate:
- ∠BAP
- ∠ADP
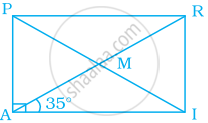
In rectangle PAIR, find ∠ARI, ∠RMI and ∠PMA.
Quadrilateral EFGH is a rectangle in which J is the point of intersection of the diagonals. Find the value of x if JF = 8x + 4 and EG = 24x – 8.
A line l is parallel to line m and a transversal p intersects them at X, Y respectively. Bisectors of interior angles at X and Y interesct at P and Q. Is PXQY a rectangle? Given reason.
