Advertisements
Advertisements
प्रश्न
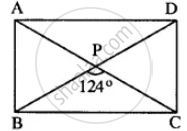
ABCD is a rectangle, if ∠BPC = 124°
Calculate:
- ∠BAP
- ∠ADP
उत्तर
Given:
- Rectangle ABCD
- ∠BPC = 124∘
Key Properties of a Rectangle:
- Diagonals of a rectangle bisect each other.
- Opposite angles formed by the diagonals are equal (angles around point P add up to 360∘).
Calculate ∠BAP:
-
In △ABP, diagonal AC divides ∠BAP and ∠BPC.
-
Since diagonals of a rectangle bisect each other, the total angles around point P are split symmetrically.
- Opposite angles: ∠BPC + ∠DPA = 180∘
Hence, ∠DPA = 180∘ − 124∘ = 56∘
Now, ∠BAP = `(∠DPA)/2`
`∠BAP = (56°)/2 = 28°`
Calculate ∠ADP:
Similarly, ∠ADP is the other half of ∠DPA:
`∠ADP = (∠DPA)/2 = 28°`
Final Answers:
- ∠BAP = 28∘
- ∠ADP = 28∘
APPEARS IN
संबंधित प्रश्न
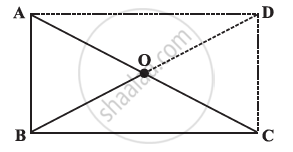
ABC is a right-angled triangle and O is the mid point of the side opposite to the right angle. Explain why O is equidistant from A, B and C. (The dotted lines are drawn additionally to help you)
Fill in the blank in the following, so as to make the statement true:
A rectangle is a parallelogram in which .....
Fill in the blank of the following, so as to make the statement true:
A square is a rectangle in which .....
The sides of a rectangle are in the ratio 2 : 3, and its perimeter is 20 cm. Draw the rectangle.
State with reason whether the following statement is ‘true’ or ‘false’.
Every parallelogram is a rectangle.
If the diagonals of a parallelogram are of equal lengths, the parallelogram is a rectangle. Prove it.
If the adjacent angles of a parallelogram are equal, then the parallelogram is a ______.
All squares are rectangles.
PQRS is a rectangle. The perpendicular ST from S on PR divides ∠S in the ratio 2:3. Find ∠TPQ.
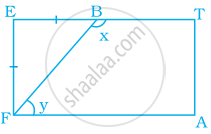
A playground is in the form of a rectangle ATEF. Two players are standing at the points F and B where EF = EB. Find the values of x and y.