Advertisements
Advertisements
प्रश्न
PQRS is a rectangle. The perpendicular ST from S on PR divides ∠S in the ratio 2:3. Find ∠TPQ.
Advertisements
उत्तर
Given, ST ⊥ PR and ST divides ∠S in the ratio 2:3
So, sum of ratio = 2 + 3 = 5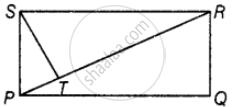
Now, `∠TSP = 2/5 xx 90^circ = 36^circ, ∠TSR = 3/5 xx 90^circ = 54^circ`
Also, by the angle sum property of a triangle,
∠TPS = 180° – (∠STP + ∠TSP)
= 180° – (90° + 36°)
= 54°
We know that, ∠SPQ = 90°
⇒ ∠TPS + ∠TPQ = 90°
⇒ 54° + ∠TPQ = 90°
⇒ ∠TPQ = 90° – 54° = 36°
APPEARS IN
संबंधित प्रश्न
Which of the following statement is true for a rectangle?
Its diagonals are perpendicular and bisect each other.
Which of the following statement are true for a square?
It has all its sides of equal length.
Which of the following statement true for a square?
Its diagonals bisect each other at right angle.
Fill in the blank in the following, so as to make the statement true:
A square is a rhombus in which .....
Draw a rectangle ABCD such that l(AB) = 6.0 cm and l (BC) = 4.5 cm.
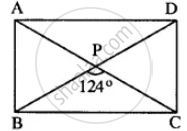
ABCD is a rectangle, if ∠BPC = 124°
Calculate:
- ∠BAP
- ∠ADP
Show that the bisectors of angles of a parallelogram form a rectangle
Rectangle is a regular quadrilateral.
Every trapezium is a rectangle.
Construct a rectangle whose one side is 3 cm and a diagonal equal to 5 cm.
