Advertisements
Advertisements
प्रश्न
If the diagonals of a parallelogram are of equal lengths, the parallelogram is a rectangle. Prove it.
उत्तर
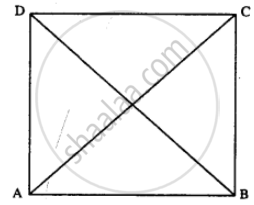
Given : //gm ABCD in which AC = BD
To Prove: ABCD is rectangle.
Proof : In ∆ABC and ∆ABD
AB = AB (Common)
AC = BD (Given)
BC = AD (opposite sides of ||gm)
∆ABC = ∆ABD (S.S.S. Rule)
∠A = ∠B
But AD // BC (opp. sides of ||gm are ||)
∠A + ∠B = 180°
∠A = ∠B = 90°
Similarly ∠D = ∠C = 90°
Hence ABCD is a rectangle.
APPEARS IN
संबंधित प्रश्न
Explain why a rectangle is a convex quadrilateral.
Which of the following statement is true for a square?
It is a rectangle.
Fill in the blank in the following, so as to make the statement true:
A rectangle is a parallelogram in which .....
Draw a rectangle whose one side measures 8 cm and the length of each of whose diagonals is 10 cm.
State with Reason Whether the Following Statement is ‘True’ Or ‘False’.
Every rectangle is a parallelogram.
Diagonals of a rectangle PQRS are intersecting in point M. If ∠QMR = 50° find the measure of ∠MPS.
Draw a rectangle ABCD such that l(AB) = 6.0 cm and l (BC) = 4.5 cm.
If the adjacent angles of a parallelogram are equal, then the parallelogram is a ______.
Every parallelogram is a rectangle.
Every trapezium is a rectangle.
