Advertisements
Advertisements
प्रश्न
In parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.
उत्तर
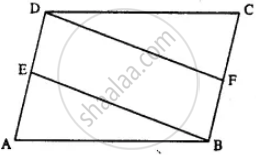
Given: Parallelogram ABCD in which E and F are mid-points of AD and BC respectively.
To Prove: BFDE is a Parallelogram.
Proof: E is the mid-point of AD. (Given)
DE = `1/2` AD
Also, F is mid-point of BC (Given)
BF = `1/2` BC
But AD = BC (opp. sides of parallelogram)
BF = DE
Again AD || BC
⇒ DE || BF
Now DE || BF and DE = BF
Hence BFDE is a parallelogram.
APPEARS IN
संबंधित प्रश्न
Consider the given parallelograms. Find the values of the unknowns x, y, z.
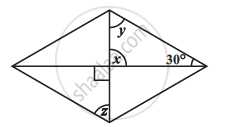
Consider the given parallelograms. Find the values of the unknowns x, y, z.
ABCD is a parallelogram. What kind of quadrilateral is it if: AC is perpendicular to BD but is not equal to it?
In parallelogram ABCD, E is the mid-point of side AB and CE bisects angle BCD. Prove that :
(i) AE = AD,
(ii) DE bisects and ∠ADC and
(iii) Angle DEC is a right angle.
The given figure shows parallelogram ABCD. Points M and N lie in diagonal BD such that DM = BN.
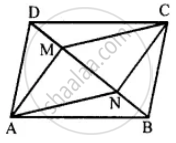
Prove that:
(i) ∆DMC = ∆BNA and so CM = AN
(ii) ∆AMD = ∆CNB and so AM CN
(iii) ANCM is a parallelogram.
Iron rods a, b, c, d, e, and f are making a design in a bridge as shown in the figure. If a || b, c || d, e || f, find the marked angles between c and f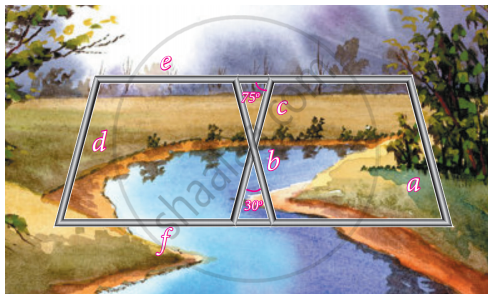
All rectangles are parallelograms.
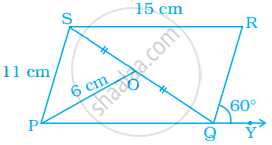
In parallelogram PQRS, O is the mid point of SQ. Find ∠S, ∠R, PQ, QR and diagonal PR.
Find the values of x and y in the following parallelogram.
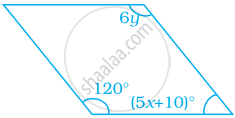
ABCD is a parallelogram. Find the value of x, y and z.

