Advertisements
Advertisements
प्रश्न
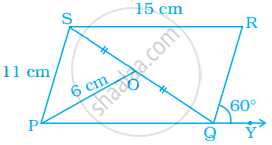
In parallelogram PQRS, O is the mid point of SQ. Find ∠S, ∠R, PQ, QR and diagonal PR.
उत्तर
Given, ∠RQY = 60°
∴ ∠RQP = 120° ...[Linear pair]
∴ ∠S = 120° ...[∵ Opposite angles are equal in a parallelogram]
By the angle sum property of a quadrilateral,
∠P + ∠R + ∠S + ∠Q = 360°
⇒ ∠P + ∠R + 120° + 120° = 360°
⇒ ∠P + ∠R + 120°
⇒ 2∠P = 120°
⇒ ∠P = 60° ...[∵ Opposite angles are equal in parallelogram]
⇒ ∠P = ∠R = 60°
Also, SR = 15 cm
∴ PQ = 15 cm ...[∵ Opposite sides of a parallelogram are equal]
And PS = 11 cm
∴ QR = 11 cm ...[∵ Opposite sides of a parallelogram are equal]
And PR = 2 × PO
= 2 × 6
= 12 cm ...[∵ Diagonals of a parallelogram bisect each other]
APPEARS IN
संबंधित प्रश्न
Consider the given parallelogram. Find the values of the unknowns x, y, z.

Can a quadrilateral ABCD be a parallelogram if ∠D + ∠B = 180°?
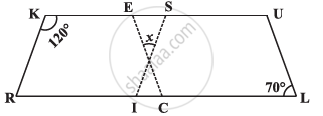
In the above figure both RISK and CLUE are parallelograms. Find the value of x.
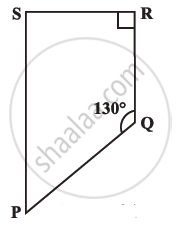
Find the measure of ∠P and ∠S, if `bar(SP) || bar(RQ)` in the following figure. (If you find m∠R, is there more than one method to find m∠P?).
Construct ☐ BARC such that l(BA) = l(BC) = 4.2 cm, l(AC) = 6.0 cm, l(AR) = l(CR) = 5.6 cm
In parallelogram ABCD, ∠A = 3 times ∠B. Find all the angles of the parallelogram. In the same parallelogram, if AB = 5x – 7 and CD = 3x +1 ; find the length of CD.
In parallelogram ABCD, E is the mid-point of side AB and CE bisects angle BCD. Prove that :
(i) AE = AD,
(ii) DE bisects and ∠ADC and
(iii) Angle DEC is a right angle.
In the following diagram, the bisectors of interior angles of the parallelogram PQRS enclose a quadrilateral ABCD.
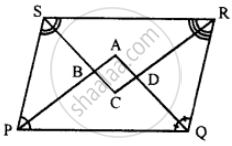
Show that:
(i) ∠PSB + ∠SPB = 90°
(ii) ∠PBS = 90°
(iii) ∠ABC = 90°
(iv) ∠ADC = 90°
(v) ∠A = 90°
(vi) ABCD is a rectangle
Thus, the bisectors of the angles of a parallelogram enclose a rectangle.
In parallelogram ABCD, X and Y are midpoints of opposite sides AB and DC respectively. Prove that:
(i) AX = YC
(ii) AX is parallel to YC
(iii) AXCY is a parallelogram.
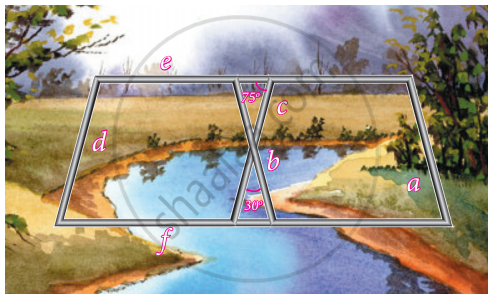
Iron rods a, b, c, d, e, and f are making a design in a bridge as shown in the figure. If a || b, c || d, e || f, find the marked angles between d and e