Advertisements
Advertisements
Question
In parallelogram PQRS, O is the mid point of SQ. Find ∠S, ∠R, PQ, QR and diagonal PR.
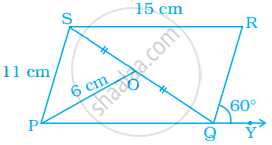
Solution
Given, ∠RQY = 60°
∴ ∠RQP = 120° ...[Linear pair]
∴ ∠S = 120° ...[∵ Opposite angles are equal in a parallelogram]
By the angle sum property of a quadrilateral,
∠P + ∠R + ∠S + ∠Q = 360°
⇒ ∠P + ∠R + 120° + 120° = 360°
⇒ ∠P + ∠R + 120°
⇒ 2∠P = 120°
⇒ ∠P = 60° ...[∵ Opposite angles are equal in parallelogram]
⇒ ∠P = ∠R = 60°
Also, SR = 15 cm
∴ PQ = 15 cm ...[∵ Opposite sides of a parallelogram are equal]
And PS = 11 cm
∴ QR = 11 cm ...[∵ Opposite sides of a parallelogram are equal]
And PR = 2 × PO
= 2 × 6
= 12 cm ...[∵ Diagonals of a parallelogram bisect each other]
APPEARS IN
RELATED QUESTIONS
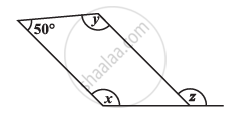
Consider the given parallelogram. Find the values of the unknowns x, y, z.
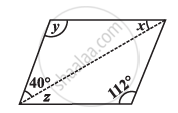
Consider the given parallelograms. Find the values of the unknowns x, y, z.
Can a quadrilateral ABCD be a parallelogram if AB = DC = 8 cm, AD = 4 cm and BC = 4.4 cm?
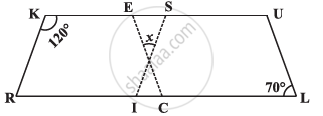
In the above figure both RISK and CLUE are parallelograms. Find the value of x.
Name the quadrilaterals whose diagonals bisect each other
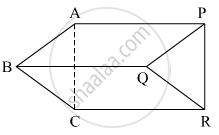
In the adjacent figure, if seg AB || seg PQ, seg AB ≅ seg PQ, seg AC || seg PR, seg AC ≅ seg PR then prove that, seg BC || seg QR and seg BC ≅ seg QR.
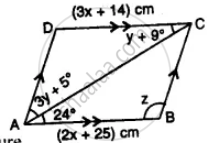
Use the information given in the alongside diagram to find the value of x, y, and z.
In the given figure, ABCD and BDCE are parallelograms with common base DC. If BC ⊥ BD, then ∠BEC = ______.

If opposite angles of a quadrilateral are equal, it must be a parallelogram.
In parallelogram ABCD, the angle bisector of ∠A bisects BC. Will angle bisector of B also bisect AD? Give reason.
