Advertisements
Advertisements
प्रश्न
In parallelogram ABCD, X and Y are midpoints of opposite sides AB and DC respectively. Prove that:
(i) AX = YC
(ii) AX is parallel to YC
(iii) AXCY is a parallelogram.
Advertisements
उत्तर
Given: In parallelogram ABCD, X and Y are the mid-points of sides AB and DC respectively AY and CX are joined.
To prove :
(i) AX = YC
(ii) AX is parallel to YC
(iii) AXCY is a parallelogram
Proof: AB || DC and X and Y are the mid-points of the sides AB and DC respectively
(i) AX = YC ( 
(ii) and AX || YC
(iii) AXCY is a parallelogram (A pair of opposite sides are equal and parallel)
Hence proved.
APPEARS IN
संबंधित प्रश्न
Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.
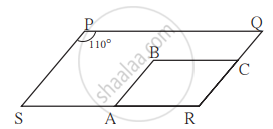
In the given figure, `square`PQRS and `square`ABCR are two parallelograms. If ∠P = 110° then find the measures of all angles of `square`ABCR.
In the given figure, `square`ABCD is a parallelogram. Point E is on the ray AB such that BE = AB then prove that line ED bisects seg BC at point F.
Construct ☐ PQRS, such that l(PQ) = 3.5 cm, l(QR) = 5.6 cm, l(RS) = 3.5 cm, m∠Q = 110°, m∠R = 70°. If it is given that ☐ PQRS is a parallelogram, which of the given information is unnecessary?
Iron rods a, b, c, d, e, and f are making a design in a bridge as shown in the figure. If a || b, c || d, e || f, find the marked angles between b and c
Iron rods a, b, c, d, e, and f are making a design in a bridge as shown in the figure. If a || b, c || d, e || f, find the marked angles between d and f
Iron rods a, b, c, d, e, and f are making a design in a bridge as shown in the figure. If a || b, c || d, e || f, find the marked angles between c and f
The angle between the two altitudes of a parallelogram through the same vertex of an obtuse angle of the parallelogram is 30°. The measure of the obtuse angle is ______.
Find the values of x and y in the following parallelogram.
The angle between the two altitudes of a parallelogram through the vertex of an obtuse angle of the parallelogram is 45°. Find the angles of the parallelogram.
