Advertisements
Advertisements
Question
In parallelogram ABCD, X and Y are midpoints of opposite sides AB and DC respectively. Prove that:
(i) AX = YC
(ii) AX is parallel to YC
(iii) AXCY is a parallelogram.
Solution
Given: In parallelogram ABCD, X and Y are the mid-points of sides AB and DC respectively AY and CX are joined.
To prove :
(i) AX = YC
(ii) AX is parallel to YC
(iii) AXCY is a parallelogram
Proof: AB || DC and X and Y are the mid-points of the sides AB and DC respectively
(i) AX = YC ( 
(ii) and AX || YC
(iii) AXCY is a parallelogram (A pair of opposite sides are equal and parallel)
Hence proved.
APPEARS IN
RELATED QUESTIONS
Consider the given parallelogram. Find the values of the unknowns x, y, z.
Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.
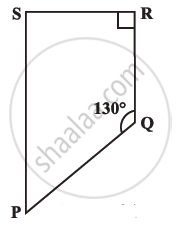
Find the measure of ∠P and ∠S, if `bar(SP) || bar(RQ)` in the following figure. (If you find m∠R, is there more than one method to find m∠P?).
Perimeter of a parallelogram is 150 cm. One of its sides is greater than the other side by 25 cm. Find the lengths of all sides.
In the given figure, G is the point of concurrence of medians of ΔDEF. Take point H on ray DG such that D-G-H and DG = GH, then prove that `square`GEHF is a parallelogram.
In the given figure, if points P, Q, R, S are on the sides of parallelogram such that AP = BQ = CR = DS then prove that `square`PQRS is a parallelogram.
Referring the adjacent figure of a parallelogram, write the answer of questions given below.
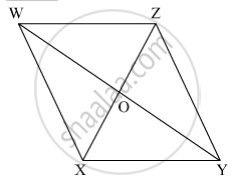
(1) If l(WZ) = 4.5 cm then l(XY) = ?
(2) If l(YZ) = 8.2 cm then l(XW) = ?
(3) If l(OX) = 2.5 cm then l(OZ) = ?
(4) If l(WO) = 3.3 cm then l(WY) = ?
(5) If m∠WZY = 120° then m∠WXY = ? and m∠XWZ = ?
ABCD is a parallelogram. What kind of quadrilateral is it if : AC = BD and AC is perpendicular to BD?
In the given figure, AB || EC, AB = AC and AE bisects ∠DAC. Prove that:
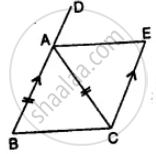
- ∠EAC = ∠ACB
- ABCE is a parallelogram.
Draw a rough figure of a quadrilateral that is not a parallelogram but has exactly two opposite angles of equal measure.
