Advertisements
Advertisements
Question
The given figure shows parallelogram ABCD. Points M and N lie in diagonal BD such that DM = BN.
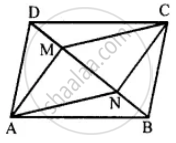
Prove that:
(i) ∆DMC = ∆BNA and so CM = AN
(ii) ∆AMD = ∆CNB and so AM CN
(iii) ANCM is a parallelogram.
Solution
Given: In parallelogram ABCD, points M and N lie on the diagonal BD such that DM = BN
AN, NC, CM and MA are joined
To prove :
(i) ∆DMC = ∆BNA and so CM = AN
(ii) ∆AMD = ∆CNB and so AM = CN
(iii) ANCM is a parallelogram
Proof :
(i) In ∆DMC and ∆BNA.
CD = AB (opposite sides of ||gm ABCD)
DM = BN (given)
∠CDM = ∠ABN (alternate angles)
∆DMC = ∆BNA (SAS axiom)
CM =AN (c.p.c.t.)
Similarly, in ∆AMD and ∆CNB
AD = BC (opposite sides of ||gm)
DM = BN (given)
∠ADM = ∠CBN – (alternate angles)
∆AMD = ∆CNB (SAS axiom)
AM = CN (c.p.c.t.)
(iii) CM = AN and AM = CN (proved)
ANCM is a parallelogram (opposite sides are equal)
Hence proved.
APPEARS IN
RELATED QUESTIONS
The measures of two adjacent angles of a parallelogram are in the ratio 3 : 2. Find the measure of each of the angles of the parallelogram.
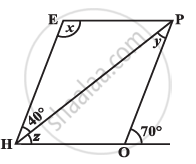
The adjacent figure HOPE is a parallelogram. Find the angle measures x, y and z. State the properties you use to find them.
Name the quadrilaterals whose diagonals bisect each other
Perimeter of a parallelogram is 150 cm. One of its sides is greater than the other side by 25 cm. Find the lengths of all sides.
In the following diagram, the bisectors of interior angles of the parallelogram PQRS enclose a quadrilateral ABCD.
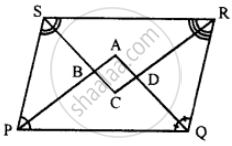
Show that:
(i) ∠PSB + ∠SPB = 90°
(ii) ∠PBS = 90°
(iii) ∠ABC = 90°
(iv) ∠ADC = 90°
(v) ∠A = 90°
(vi) ABCD is a rectangle
Thus, the bisectors of the angles of a parallelogram enclose a rectangle.
Iron rods a, b, c, d, e, and f are making a design in a bridge as shown in the figure. If a || b, c || d, e || f, find the marked angles between d and e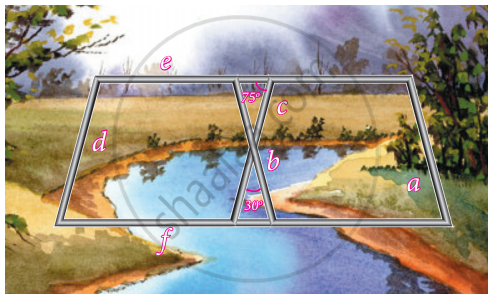
In the given figure, ABCD and BDCE are parallelograms with common base DC. If BC ⊥ BD, then ∠BEC = ______.

In parallelogram LOST, SN ⊥ OL and SM ⊥ LT. Find ∠STM, ∠SON and ∠NSM.

In parallelogram MODE, the bisector of ∠M and ∠O meet at Q, find the measure of ∠MQO.
ABCD is a parallelogram. Points P and Q are taken on the sides AB and AD respectively and the parallelogram PRQA is formed. If ∠C = 45°, find ∠R.
