Advertisements
Advertisements
Question
The measures of two adjacent angles of a parallelogram are in the ratio 3 : 2. Find the measure of each of the angles of the parallelogram.
Solution
Let the measures of two adjacent angles, ∠A and ∠B, of parallelogram ABCD are in the ratio of 3 : 2. Let ∠A = 3x and ∠B = 2x
We know that the sum of the measures of adjacent angles is 180º for a parallelogram.
∠A + ∠B = 180º
3x + 2x = 180º
5x = 180º
`x = 180^circ/5 = 36`
∠A = ∠C = 3x = 108º (Opposite angles)
∠B = ∠D = 2x = 72º (Opposite angles)
Thus, the measures of the angles of the parallelogram are 108º, 72º, 108º, and 72º
APPEARS IN
RELATED QUESTIONS
Can a quadrilateral ABCD be a parallelogram if ∠D + ∠B = 180°?
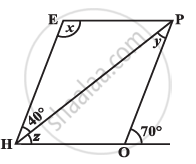
The adjacent figure HOPE is a parallelogram. Find the angle measures x, y and z. State the properties you use to find them.
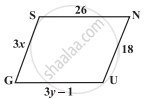
The following figure GUNS is a parallelogram. Find x and y. (Lengths are in cm)
If the ratio of measures of two adjacent angles of a parallelogram is 1 : 2, find the measures of all angles of the parallelogram.
Given: Parallelogram ABCD in which diagonals AC and BD intersect at M.
Prove: M is the mid-point of LN.
In parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.
Which of the following figures satisfy the following properties?
- All sides are congruent.
- All angles are right angles.
- Opposite sides are parallel.
All rectangles are parallelograms.
A diagonal of a parallelogram bisects an angle. Will it also bisect the other angle? Give reason.
Construct a parallelogram ABCD in which AB = 4 cm, BC = 5 cm and ∠B = 60°.
