Advertisements
Advertisements
प्रश्न
The measures of two adjacent angles of a parallelogram are in the ratio 3 : 2. Find the measure of each of the angles of the parallelogram.
उत्तर
Let the measures of two adjacent angles, ∠A and ∠B, of parallelogram ABCD are in the ratio of 3 : 2. Let ∠A = 3x and ∠B = 2x
We know that the sum of the measures of adjacent angles is 180º for a parallelogram.
∠A + ∠B = 180º
3x + 2x = 180º
5x = 180º
`x = 180^circ/5 = 36`
∠A = ∠C = 3x = 108º (Opposite angles)
∠B = ∠D = 2x = 72º (Opposite angles)
Thus, the measures of the angles of the parallelogram are 108º, 72º, 108º, and 72º
APPEARS IN
संबंधित प्रश्न
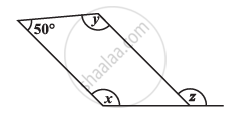
Consider the given parallelogram. Find the values of the unknowns x, y, z.
Name the quadrilaterals whose diagonals bisect each other
Perimeter of a parallelogram is 150 cm. One of its sides is greater than the other side by 25 cm. Find the lengths of all sides.
Construct ☐ PQRS, such that l(PQ) = 3.5 cm, l(QR) = 5.6 cm, l(RS) = 3.5 cm, m∠Q = 110°, m∠R = 70°. If it is given that ☐ PQRS is a parallelogram, which of the given information is unnecessary?
ABCD is a parallelogram. What kind of quadrilateral is it if: AC = BD but AC is not perpendicular to BD?
Prove that the diagonals of a parallelogram bisect each other.
In parallelogram ABCD, E is the mid-point of side AB and CE bisects angle BCD. Prove that :
(i) AE = AD,
(ii) DE bisects and ∠ADC and
(iii) Angle DEC is a right angle.
If two adjacent angles of a parallelogram are (5x – 5)° and (10x + 35)°, then the ratio of these angles is ______.
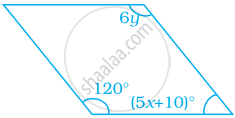
Find the values of x and y in the following parallelogram.
In parallelogram ABCD, the angle bisector of ∠A bisects BC. Will angle bisector of B also bisect AD? Give reason.
