Advertisements
Advertisements
प्रश्न
In parallelogram ABCD, E is the mid-point of side AB and CE bisects angle BCD. Prove that :
(i) AE = AD,
(ii) DE bisects and ∠ADC and
(iii) Angle DEC is a right angle.
उत्तर
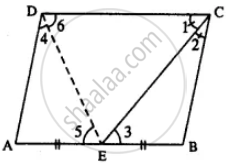
Given: parallelogram ABCD in which E is mid-point of AB and CE bisects ZBCD.
To Prove :
(i) AE = AD
(ii) DE bisects ∠ADC
(iii) ∠DEC = 90°
Const. Join DE
Proof : (i) AB || CD (Given)
and CE bisects it.
∠1 = ∠3 (alternate ∠s) ……… (i)
But ∠1 = ∠2 (Given) …………. (ii)
From (i) & (ii)
∠2 = ∠3
BC = BE (sides opp. to equal angles)
But BC = AD (opp. sides of ||gm)
and BE = AE (Given)
AD = AE
∠4 = ∠5 (∠s opp. to equal sides)
But ∠5 = ∠6 (alternate ∠s)
=> ∠4 = ∠6
DE bisects ∠ADC.
Now AD || BC
=> ∠D + ∠C = 180°
2∠6+2∠1 = 180°
DE and CE are bisectors.
∠6 + ∠1 = `180^circ/2`
∠6 + ∠1 = 90°
But ∠DEC + ∠6 + ∠1 = 180°
∠DEC + 90° = 180°
∠DEC = 180° – 90°
∠DEC = 90°
Hence the result.
APPEARS IN
संबंधित प्रश्न
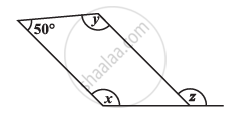
Consider the given parallelogram. Find the values of the unknowns x, y, z.
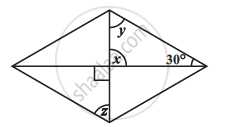
Consider the given parallelograms. Find the values of the unknowns x, y, z.
Can a quadrilateral ABCD be a parallelogram if ∠D + ∠B = 180°?
Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.
Perimeter of a parallelogram is 150 cm. One of its sides is greater than the other side by 25 cm. Find the lengths of all sides.
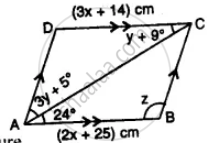
Use the information given in the alongside diagram to find the value of x, y, and z.
Which of the following figures satisfy the following properties?
- All sides are congruent.
- All angles are right angles.
- Opposite sides are parallel.
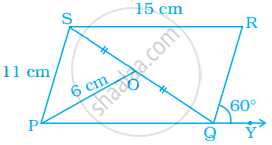
In parallelogram PQRS, O is the mid point of SQ. Find ∠S, ∠R, PQ, QR and diagonal PR.
Two angles of a quadrilateral are each of measure 75° and the other two angles are equal. What is the measure of these two angles? Name the possible figures so formed.
Construct a parallelogram when one of its side is 4 cm and its two diagonals are 5.6 cm and 7 cm. Measure the other side.
