Advertisements
Advertisements
प्रश्न
In the following diagram, the bisectors of interior angles of the parallelogram PQRS enclose a quadrilateral ABCD.
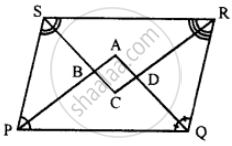
Show that:
(i) ∠PSB + ∠SPB = 90°
(ii) ∠PBS = 90°
(iii) ∠ABC = 90°
(iv) ∠ADC = 90°
(v) ∠A = 90°
(vi) ABCD is a rectangle
Thus, the bisectors of the angles of a parallelogram enclose a rectangle.
उत्तर
Given: In parallelogram ABCD bisector of angles P and Q, meet at A, bisectors of ∠R and ∠S meet at C. Forming a quadrilateral ABCD as shown in the figure.
To prove :
(i) ∠PSB + ∠SPB = 90°
(ii) ∠PBS = 90°
(iii) ∠ABC = 90°
(iv) ∠ADC = 90°
(v) ∠A = 9°
(vi) ABCD is a rectangle
Proof : In parallelogram PQRS,
PS || QR (opposite sides)
(i) ∠P +∠Q = 180°
= `(∠P)/2 + (∠S)/2 = 90°`
= ∠SPB + ∠PSB = 90°`
(ii) In tringle ∠PBS = 90°
∠SPB + ∠PSB + ∠PBS = 180°
= 90° + ∠PSB = 180°
= ∠PSB = 90°
(iii) ∠ABC = 90°
∠PBS = ∠ABC {vertically opposite}
∠ABC = 90°
(iv) In ∠ADC = 90°
`R/2 + Q/2 + RDQ = 180°`
RDQ = 180 - 90
RDQ = 90°
∴ ∠ADC = 90° {vertically opposite}
(v) ∠A = 90°
Similarly PQ || SR
∠PSB + SPB = 90°
(vi) ABCD is a rectangle (Each angle of a quadrilateral is 90°)
Hence proved.
APPEARS IN
संबंधित प्रश्न
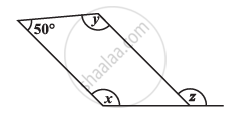
Consider the given parallelogram. Find the values of the unknowns x, y, z.
Can a quadrilateral ABCD be a parallelogram if AB = DC = 8 cm, AD = 4 cm and BC = 4.4 cm?
Name the quadrilaterals whose diagonals bisect each other
Perimeter of a parallelogram is 150 cm. One of its sides is greater than the other side by 25 cm. Find the lengths of all sides.
In the adjacent figure, if seg AB || seg PQ, seg AB ≅ seg PQ, seg AC || seg PR, seg AC ≅ seg PR then prove that, seg BC || seg QR and seg BC ≅ seg QR.
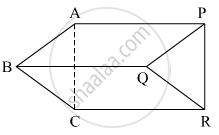
In parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.
In the given figure, ABCD and BDCE are parallelograms with common base DC. If BC ⊥ BD, then ∠BEC = ______.

In parallelogram MODE, the bisector of ∠M and ∠O meet at Q, find the measure of ∠MQO.
ABCD is a parallelogram. Find the value of x, y and z.

In parallelogram ABCD, the angle bisector of ∠A bisects BC. Will angle bisector of B also bisect AD? Give reason.
