Advertisements
Advertisements
प्रश्न
In the following diagram, the bisectors of interior angles of the parallelogram PQRS enclose a quadrilateral ABCD.
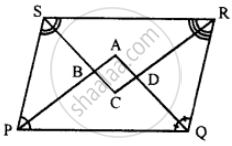
Show that:
(i) ∠PSB + ∠SPB = 90°
(ii) ∠PBS = 90°
(iii) ∠ABC = 90°
(iv) ∠ADC = 90°
(v) ∠A = 90°
(vi) ABCD is a rectangle
Thus, the bisectors of the angles of a parallelogram enclose a rectangle.
उत्तर
Given: In parallelogram ABCD bisector of angles P and Q, meet at A, bisectors of ∠R and ∠S meet at C. Forming a quadrilateral ABCD as shown in the figure.
To prove :
(i) ∠PSB + ∠SPB = 90°
(ii) ∠PBS = 90°
(iii) ∠ABC = 90°
(iv) ∠ADC = 90°
(v) ∠A = 9°
(vi) ABCD is a rectangle
Proof : In parallelogram PQRS,
PS || QR (opposite sides)
(i) ∠P +∠Q = 180°
= `(∠P)/2 + (∠S)/2 = 90°`
= ∠SPB + ∠PSB = 90°`
(ii) In tringle ∠PBS = 90°
∠SPB + ∠PSB + ∠PBS = 180°
= 90° + ∠PSB = 180°
= ∠PSB = 90°
(iii) ∠ABC = 90°
∠PBS = ∠ABC {vertically opposite}
∠ABC = 90°
(iv) In ∠ADC = 90°
`R/2 + Q/2 + RDQ = 180°`
RDQ = 180 - 90
RDQ = 90°
∴ ∠ADC = 90° {vertically opposite}
(v) ∠A = 90°
Similarly PQ || SR
∠PSB + SPB = 90°
(vi) ABCD is a rectangle (Each angle of a quadrilateral is 90°)
Hence proved.
APPEARS IN
संबंधित प्रश्न
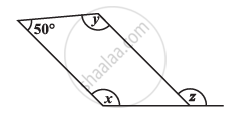
Consider the given parallelogram. Find the values of the unknowns x, y, z.
Name the quadrilaterals whose diagonals bisect each other
If the ratio of measures of two adjacent angles of a parallelogram is 1 : 2, find the measures of all angles of the parallelogram.
Ratio of consecutive angles of a quadrilateral is 1 : 2 : 3 : 4. Find the measure of its each angle. Write, with reason, what type of a quadrilateral it is.
Referring the adjacent figure of a parallelogram, write the answer of questions given below.
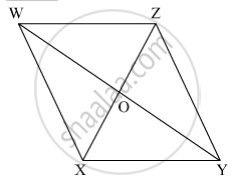
(1) If l(WZ) = 4.5 cm then l(XY) = ?
(2) If l(YZ) = 8.2 cm then l(XW) = ?
(3) If l(OX) = 2.5 cm then l(OZ) = ?
(4) If l(WO) = 3.3 cm then l(WY) = ?
(5) If m∠WZY = 120° then m∠WXY = ? and m∠XWZ = ?
ABCD is a parallelogram. What kind of quadrilateral is it if: AC is perpendicular to BD but is not equal to it?
Which of the following figures satisfy the following properties?
- All sides are congruent.
- All angles are right angles.
- Opposite sides are parallel.
In the given figure, ABCD and BDCE are parallelograms with common base DC. If BC ⊥ BD, then ∠BEC = ______.

The adjacent sides of a parallelogram are 5 cm and 9 cm. Its perimeter is ______.
ABCD is a parallelogram. Find the value of x, y and z.

