Advertisements
Advertisements
प्रश्न
If the ratio of measures of two adjacent angles of a parallelogram is 1 : 2, find the measures of all angles of the parallelogram.
उत्तर
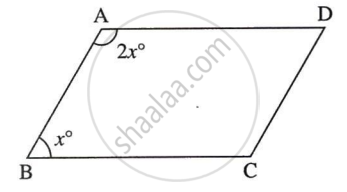
Let `square`ABCD be the parallelogram.
The ratio of measures of two adjacent angles of a parallelogram is 1 : 2.
Let the common multiple be x.
∴ ∠A = x° and ∠B = 2x°
∠A + ∠B = 180° ...[Adjacent angles of a parallelogram are supplementary]
∴ x + 2x = 180
∴ 3x = 180
∴ x = `180/3`
∴ x = 60
∠A = x° = 60°
∠B = 2x°
= 2 × 60° = 120°
∠A = ∠C = 60°
∠B = ∠D= 120° ...[Opposite angles of a parallelogram]
APPEARS IN
संबंधित प्रश्न
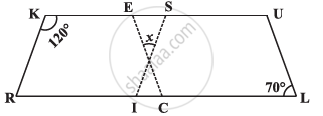
In the above figure both RISK and CLUE are parallelograms. Find the value of x.
In the adjacent figure, if seg AB || seg PQ, seg AB ≅ seg PQ, seg AC || seg PR, seg AC ≅ seg PR then prove that, seg BC || seg QR and seg BC ≅ seg QR.
Construct ☐ PQRS, such that l(PQ) = 3.5 cm, l(QR) = 5.6 cm, l(RS) = 3.5 cm, m∠Q = 110°, m∠R = 70°. If it is given that ☐ PQRS is a parallelogram, which of the given information is unnecessary?
Given: Parallelogram ABCD in which diagonals AC and BD intersect at M.
Prove: M is the mid-point of LN.
In parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.
In parallelogram ABCD, E is the mid-point of side AB and CE bisects angle BCD. Prove that :
(i) AE = AD,
(ii) DE bisects and ∠ADC and
(iii) Angle DEC is a right angle.
The given figure shows parallelogram ABCD. Points M and N lie in diagonal BD such that DM = BN.
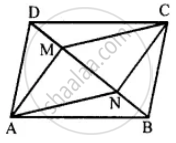
Prove that:
(i) ∆DMC = ∆BNA and so CM = AN
(ii) ∆AMD = ∆CNB and so AM CN
(iii) ANCM is a parallelogram.
In parallelogram PQRS, O is the mid point of SQ. Find ∠S, ∠R, PQ, QR and diagonal PR.
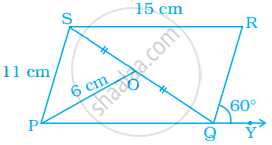
In the following figure, FD || BC || AE and AC || ED. Find the value of x.
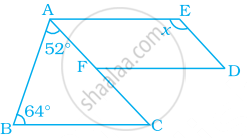
Draw a rough figure of a quadrilateral that is not a parallelogram but has exactly two opposite angles of equal measure.
