Balbharati solutions for Geometry (Mathematics 2) [English] 9 Standard Maharashtra State Board chapter 5 - Quadrilaterals [Latest edition]

Diagonals of a parallelogram `square`WXYZ intersect each other at point O. If ∠XYZ = 135° then what is the measure of ∠XWZ and ∠YZW? 

If l(OY)= 5 cm then l(WY)= ?

In a parallelogram `square`ABCD, If ∠A = (3x + 12)°, ∠B = (2x - 32)° then find the value of x and then find the measures of ∠C and ∠D. 

Perimeter of a parallelogram is 150 cm. One of its sides is greater than the other side by 25 cm. Find the lengths of all sides.

If the ratio of measures of two adjacent angles of a parallelogram is 1 : 2, find the measures of all angles of the parallelogram.

Diagonals of a parallelogram intersect each other at point O. If AO = 5, BO = 12 and AB = 13 then show that `square`ABCD is a rhombus. 

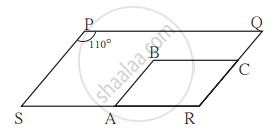
In the given figure, `square`PQRS and `square`ABCR are two parallelograms. If ∠P = 110° then find the measures of all angles of `square`ABCR.

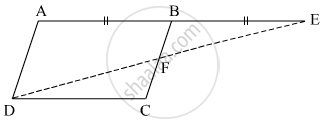
In the given figure, `square`ABCD is a parallelogram. Point E is on the ray AB such that BE = AB then prove that line ED bisects seg BC at point F.

`square`ABCD is a parallelogram, P and Q are midpoints of side AB and DC respectively, then prove `square`APCQ is a parallelogram.

Using opposite angles test for parallelogram, prove that every rectangle is a parallelogram.

In the given figure, G is the point of concurrence of medians of ΔDEF. Take point H on ray DG such that D-G-H and DG = GH, then prove that `square`GEHF is a parallelogram.

Prove that quadrilateral formed by the intersection of angle bisectors of all angles of a parallelogram is a rectangle.

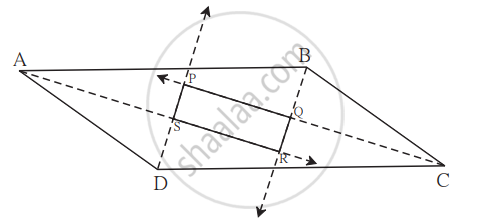
In the given figure, if points P, Q, R, S are on the sides of parallelogram such that AP = BQ = CR = DS then prove that `square`PQRS is a parallelogram.

Diagonals of a rectangle ABCD intersect at point O. If AC = 8 cm then find BO and if ∠CAD =35°  then find ∠ACB.

In a rhombus PQRS if PQ = 7.5 cm then find QR. If ∠QPS = 75° then find the measure of ∠PQR and ∠SRQ.

Diagonals of a square IJKL intersects at point M, Find the measures of ∠IMJ, ∠JIK and ∠LJK .

Diagonals of a rhombus are 20 cm and 21 cm respectively, then find the side of rhombus and its perimeter.

State with reason whether the following statement is ‘true’ or ‘false’.

Every parallelogram is a rhombus.

State with reason whether the following statement is ‘true’ or ‘false’.

Every rhombus is a rectangle.

State with Reason Whether the Following Statement is ‘True’ Or ‘False’.

Every rectangle is a parallelogram.

State with reason whether the following statement is ‘true’ or ‘false’.

Every square is a rectangle.

State with reason whether the following statement is ‘true’ or ‘false’.

Every square is a rhombus.

State with reason whether the following statement is ‘true’ or ‘false’.

Every parallelogram is a rectangle.

In `square` IJKL, side IJ || side KL, ∠I = 108°, ∠K = 53° then find the measure of ∠J and ∠L.

In `square`ABCD, side BC || side AD, side AB ≅ side DC If ∠A = 72° then find the measure of ∠B and ∠D.

In `square`ABCD, side BC < side AD in following figure. side BC || side AD and if side BA ≅ side CD then prove that ∠ABC ≅ ∠DCB.

In the given figure, points X, Y, Z are the midpoints of side AB, side BC and side AC of ΔABC respectively. AB = 5 cm, AC = 9 cm and BC = 11 cm. Find the length of XY, YZ, XZ.

In the given figure, `square`PQRS and `square`MNRL are rectangles. If point M is the midpoint of side PR then prove that,

1. SL = LR
2. LN = `1/2`SQ

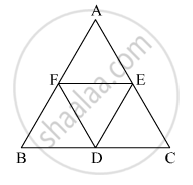
In the given figure, ΔABC is an equilateral traingle. Points F, D and E are midpoints of side AB, side BC, side AC respectively. Show that ΔFED is an equilateral traingle.

In the given figure, seg PD is a median of ΔPQR. Point T is the mid point of seg PD. Produced QT intersects PR at M. Show that `"PM"/"PR" = 1/3`.

[Hint: DN || QM]

If all pairs of adjacent sides of a quadrilateral are congruent then it is called ______.

If the diagonal of a square is `12 sqrt 2` cm then the perimeter of square is ______.

If opposite angles of a rhombus are (2x)° and (3x - 40)° then value of x is ______.

Adjacent sides of a rectangle are 7 cm and 24 cm. Find the length of its diagonal.

If diagonal of a square is 13 cm then find its side.

Ratio of two adjacent sides of a parallelogram is 3 : 4, and its perimeter is 112 cm. Find the length of its each side.

Diagonals PR and QS of a rhombus PQRS are 20 cm and 48 cm respectively. Find the length of side PQ.

Diagonals of a rectangle PQRS are intersecting in point M. If ∠QMR = 50° find the measure of ∠MPS.

In the adjacent figure, if seg AB || seg PQ, seg AB ≅ seg PQ, seg AC || seg PR, seg AC ≅ seg PR then prove that, seg BC || seg QR and seg BC ≅ seg QR.

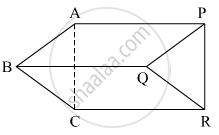
In the Figure, `square`ABCD is a trapezium. AB || DC. Points P and Q are midpoints of seg AD and seg BC respectively. Then prove that, PQ || AB and PQ = `1/2 ("AB" + "DC")`.

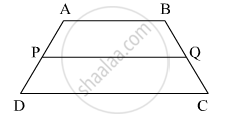
In the adjacent figure, `square`ABCD is a trapezium AB || DC. Points M and N are midpoints of diagonal AC and DB respectively then prove that MN || AB.