Advertisements
Advertisements
प्रश्न
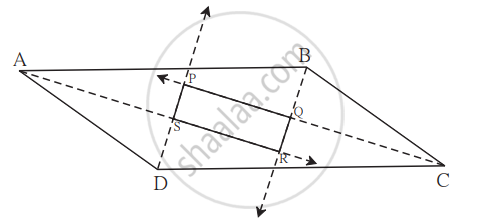
Prove that quadrilateral formed by the intersection of angle bisectors of all angles of a parallelogram is a rectangle.
उत्तर
Given: `square`ABCD is a parallelogram.
To prove: `square`PQRS is a rectangle.
Proof:
`square`ABCD is a parallelogram. ...(Given)
∠ADC + ∠BCD = 180° ...(Adjacent angles of a parallelogram are supplementary.)
Multiplying each side by `1/2`,
`1/2` ∠ADC + `1/2` ∠BCD = `1/2xx180°` ...(i)
But,
`1/2` ∠ADC = ∠PDC ...(Ray DP bisects ∠ADC) ...(ii)
And `1/2` ∠BCD = ∠PCD ...(Ray CP bisects ∠BCD) ...(iii)
∴ ∠PDC + ∠PCD = 90° ...[From (i), (ii) and (iii)] ...(iv)
In ΔPDC,
∠PDC + ∠PCD + ∠DPC = 180° ...(The sum of the measures of the three angles of a triangle is 180°.)
∴ 90° + ∠DPC = 180° ...[from (iv)]
∴ ∠DPC = 180° – 90°
∴ ∠DPC = 90°
That means ∠SPQ = 90° ...(D-S-P, P-Q-C) ...(v)
Similarly, we can prove that, ∠SRQ = 90° ...(vi)
Similarly, ∠ASD = 90° and ∠BQC = 90° ...(vii)
∠PSR = ∠ASD ...(vertex angle)
∴ ∠PSR = 90° ...[From (vii)] ...(viii)
Similarly, ∠PQR = 90° ...(ix)
In `square`PQRS,
∠SPQ = ∠SRQ = ∠PSR = ∠PQR = 90° ...[From (v), (vi), (viii) and (ix)]
∴ `square`PQRS is a rectangle.
APPEARS IN
संबंधित प्रश्न
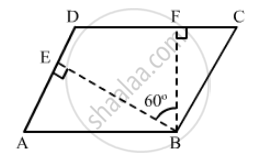
The angle between the altitudes of a parallelogram, through the same vertex of an obtuse angle of the parallelogram is 60°. Find the angles of the parallelogram.
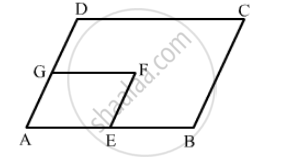
In the following figure, ABCD and AEFG are parallelograms. If ∠C = 55°, what is the measure of ∠F?
Fill in the blank in the following, so as to make the statement true:
A rectangle is a parallelogram in which .....
Draw a square whose each side measures 4.8 cm.
A mason has made a concrete slab. He needs it to be rectangular. In what different ways can he make sure that it is rectangular?
Draw a rectangle ABCD such that l(AB) = 6.0 cm and l (BC) = 4.5 cm.
The following figure is a rectangle in which x: y = 3: 7; find the values of x and y.
If the diagonals of a quadrilateral are equal and bisect each other, then the quadrilateral is a ______.
Every trapezium is a rectangle.
A rectangular MORE is shown below:
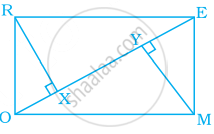
Answer the following questions by giving appropriate reason.
- Is RE = OM?
- Is ∠MYO = ∠RXE?
- Is ∠MOY = ∠REX?
- Is ΔMYO ≅ ΔRXE?
- Is MY = RX?
