Advertisements
Advertisements
प्रश्न
In the given figure, G is the point of concurrence of medians of ΔDEF. Take point H on ray DG such that D-G-H and DG = GH, then prove that `square`GEHF is a parallelogram.

उत्तर
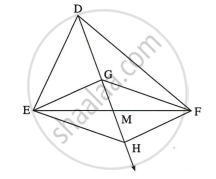
Let, the median side drawn from point D intersects EF at point M.
Point G is the concurrence point.
The concurrence point divides each median in the ratio 2:1.
∴ DG : GM = 2 : 1
∴ `("DG")/("GM") = 2/1`
∴ DG = 2GM ...(i)
∴ DG = GM + MH ...(G-M-H)
∴ 2GM = GM + MH ...[from (i)]
∴ 2GM – GM = MH
∴ GM = MH ...(ii)
In `square`GEHF,
Line GM ≅ Line MH ...[From (ii)]
Line EM ≅ Line MF ...(Point M is the midpoint of line EF)
A quadrilateral is a parallelogram if its diagonals bisect each other.
`square`GEHF is a parallelogram.
APPEARS IN
संबंधित प्रश्न
Can a quadrilateral ABCD be a parallelogram if ∠D + ∠B = 180°?
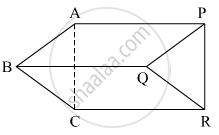
In the adjacent figure, if seg AB || seg PQ, seg AB ≅ seg PQ, seg AC || seg PR, seg AC ≅ seg PR then prove that, seg BC || seg QR and seg BC ≅ seg QR.
In parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.
In the following diagram, the bisectors of interior angles of the parallelogram PQRS enclose a quadrilateral ABCD.
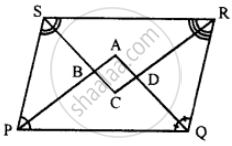
Show that:
(i) ∠PSB + ∠SPB = 90°
(ii) ∠PBS = 90°
(iii) ∠ABC = 90°
(iv) ∠ADC = 90°
(v) ∠A = 90°
(vi) ABCD is a rectangle
Thus, the bisectors of the angles of a parallelogram enclose a rectangle.
In parallelogram ABCD, X and Y are midpoints of opposite sides AB and DC respectively. Prove that:
(i) AX = YC
(ii) AX is parallel to YC
(iii) AXCY is a parallelogram.
In parallelogram LOST, SN ⊥ OL and SM ⊥ LT. Find ∠STM, ∠SON and ∠NSM.

In parallelogram MODE, the bisector of ∠M and ∠O meet at Q, find the measure of ∠MQO.
Two angles of a quadrilateral are each of measure 75° and the other two angles are equal. What is the measure of these two angles? Name the possible figures so formed.
Construct a parallelogram HOME with HO = 6 cm, HE = 4 cm and OE = 3 cm.
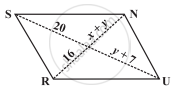
The following figure RUNS is parallelogram. Find x and y. (Lengths are in cm)