Advertisements
Advertisements
प्रश्न
In the given figure, G is the point of concurrence of medians of ΔDEF. Take point H on ray DG such that D-G-H and DG = GH, then prove that `square`GEHF is a parallelogram.

उत्तर
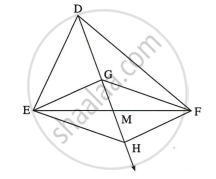
Let, the median side drawn from point D intersects EF at point M.
Point G is the concurrence point.
The concurrence point divides each median in the ratio 2:1.
∴ DG : GM = 2 : 1
∴ `("DG")/("GM") = 2/1`
∴ DG = 2GM ...(i)
∴ DG = GM + MH ...(G-M-H)
∴ 2GM = GM + MH ...[from (i)]
∴ 2GM – GM = MH
∴ GM = MH ...(ii)
In `square`GEHF,
Line GM ≅ Line MH ...[From (ii)]
Line EM ≅ Line MF ...(Point M is the midpoint of line EF)
A quadrilateral is a parallelogram if its diagonals bisect each other.
`square`GEHF is a parallelogram.
APPEARS IN
संबंधित प्रश्न
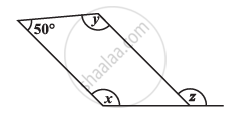
Consider the given parallelogram. Find the values of the unknowns x, y, z.

Consider the given parallelogram. Find the values of the unknowns x, y, z.
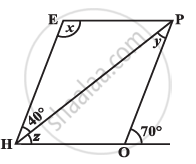
The adjacent figure HOPE is a parallelogram. Find the angle measures x, y and z. State the properties you use to find them.
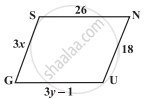
The following figure GUNS is a parallelogram. Find x and y. (Lengths are in cm)
Find the measure of ∠P and ∠S, if `bar(SP) || bar(RQ)` in the following figure. (If you find m∠R, is there more than one method to find m∠P?).
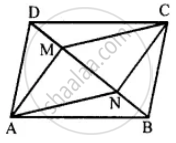
Given: Parallelogram ABCD in which diagonals AC and BD intersect at M.
Prove: M is the mid-point of LN.
The given figure shows parallelogram ABCD. Points M and N lie in diagonal BD such that DM = BN.
Prove that:
(i) ∆DMC = ∆BNA and so CM = AN
(ii) ∆AMD = ∆CNB and so AM CN
(iii) ANCM is a parallelogram.
Which of the following figures satisfy the following properties?
- All sides are congruent.
- All angles are right angles.
- Opposite sides are parallel.
All rectangles are parallelograms.
In parallelogram MODE, the bisector of ∠M and ∠O meet at Q, find the measure of ∠MQO.
