Advertisements
Advertisements
प्रश्न
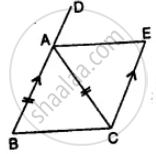
Given: Parallelogram ABCD in which diagonals AC and BD intersect at M.
Prove: M is the mid-point of LN.
उत्तर

Proof: Diagonals of //gm bisect each other.
MD = MB
Also ∠ADB = ∠DBN (Alternate ∠s)
& ∠DML = ∠BMN (Vert. opp. ∠s)
∆DML = ∆BMN
LM = MN
M is mid-point of LN.
Hence proved.
APPEARS IN
संबंधित प्रश्न
Consider the given parallelogram. Find the values of the unknowns x, y, z.

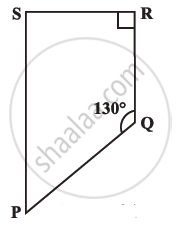
Find the measure of ∠P and ∠S, if `bar(SP) || bar(RQ)` in the following figure. (If you find m∠R, is there more than one method to find m∠P?).
Ratio of two adjacent sides of a parallelogram is 3 : 4, and its perimeter is 112 cm. Find the length of its each side.
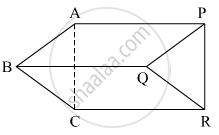
In the adjacent figure, if seg AB || seg PQ, seg AB ≅ seg PQ, seg AC || seg PR, seg AC ≅ seg PR then prove that, seg BC || seg QR and seg BC ≅ seg QR.
Prove that the diagonals of a parallelogram bisect each other.
In the given figure, AB || EC, AB = AC and AE bisects ∠DAC. Prove that:
- ∠EAC = ∠ACB
- ABCE is a parallelogram.
If a triangle and a parallelogram lie on the same base and between the same parallels, then prove that the area of the triangle is equal to half of the area of parallelogram
The adjacent sides of a parallelogram are 5 cm and 9 cm. Its perimeter is ______.
A diagonal of a parallelogram bisects an angle. Will it also bisect the other angle? Give reason.
Draw a rough figure of a quadrilateral that is not a parallelogram but has exactly two opposite angles of equal measure.
