Advertisements
Advertisements
Question
Given: Parallelogram ABCD in which diagonals AC and BD intersect at M.
Prove: M is the mid-point of LN.
Solution

Proof: Diagonals of //gm bisect each other.
MD = MB
Also ∠ADB = ∠DBN (Alternate ∠s)
& ∠DML = ∠BMN (Vert. opp. ∠s)
∆DML = ∆BMN
LM = MN
M is mid-point of LN.
Hence proved.
APPEARS IN
RELATED QUESTIONS
Given a parallelogram ABCD. Complete each statement along with the definition or property used.
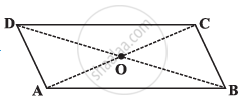
- AD = ______
- ∠DCB = ______
- OC = ______
- m∠DAB + m∠CDA = ______
Can a quadrilateral ABCD be a parallelogram if AB = DC = 8 cm, AD = 4 cm and BC = 4.4 cm?
Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.
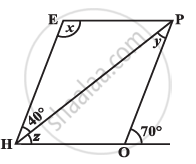
The adjacent figure HOPE is a parallelogram. Find the angle measures x, y and z. State the properties you use to find them.
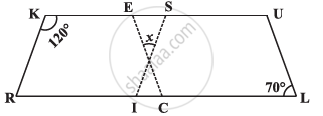
In the above figure both RISK and CLUE are parallelograms. Find the value of x.
Perimeter of a parallelogram is 150 cm. One of its sides is greater than the other side by 25 cm. Find the lengths of all sides.
In the given figure, if points P, Q, R, S are on the sides of parallelogram such that AP = BQ = CR = DS then prove that `square`PQRS is a parallelogram.

In parallelogram ABCD, ∠A = 3 times ∠B. Find all the angles of the parallelogram. In the same parallelogram, if AB = 5x – 7 and CD = 3x +1 ; find the length of CD.
Two angles of a quadrilateral are each of measure 75° and the other two angles are equal. What is the measure of these two angles? Name the possible figures so formed.
ABCD is a parallelogram. Points P and Q are taken on the sides AB and AD respectively and the parallelogram PRQA is formed. If ∠C = 45°, find ∠R.
