Advertisements
Advertisements
Question
In an Isosceles-trapezium, show that the opposite angles are supplementary.
Solution
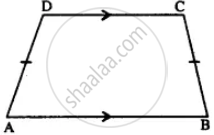
Given : ABCD is isosceles trapezium in which AD = BC
To Prove :
(i) ∠A + ∠C = 180°
(ii) ∠B + ∠D = 180°
Proof : AB || CD.
⇒ ∠A + ∠D = 180°
But ∠A = ∠B [Trapezium is isosceles)]
∠B + ∠D = 180°
Similarly ∠A + ∠C = 180°
Hence the result.
APPEARS IN
RELATED QUESTIONS
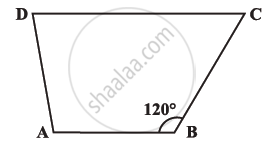
Explain how this figure is a trapezium. Which of its two sides are parallel?
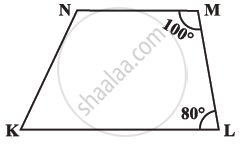
Find m∠C in the following figure if `bar(AB) || bar(DC)`
All parallelograms are trapeziums.
All squares are trapeziums.
In `square` IJKL, side IJ || side KL, ∠I = 108°, ∠K = 53° then find the measure of ∠J and ∠L.
A quadrilateral in which a pair of opposite sides is parallel is ______.
Every rhombus is a trapezium.
In a quadrilateral HOPE, PS and ES are bisectors of ∠P and ∠E respectively. Give reason.
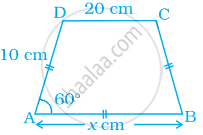
In the following figure, AB || DC and AD = BC. Find the value of x.
Construct a trapezium ABCD where AB || CD, AD = BC = 3.2 cm, AB = 6.4 cm and CD = 9.6 cm. Measure ∠B and ∠A.
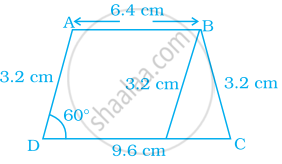
[Hint: Difference of two parallel sides gives an equilateral triangle.]
