Selina solutions for Concise Mathematics [English] Class 8 ICSE chapter 17 - Special Types of Quadrilaterals [Latest edition]

In parallelogram ABCD, ∠A = 3 times ∠B. Find all the angles of the parallelogram. In the same parallelogram, if AB = 5x – 7 and CD = 3x +1 ; find the length of CD.

In parallelogram PQRS, ∠Q = (4x – 5)° and ∠S = (3x + 10)°. Calculate: ∠Q and ∠R.

In rhombus ABCD;
(i) if ∠A = 74° ; find ∠B and ∠C.
(ii) if AD = 7.5 cm ; find BC and CD.

In square PQRS :
(i) if PQ = 3x – 7 and QR = x + 3 ; find PS
(ii) if PR = 5x and QS = 9x – 8. Find QS

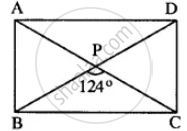
ABCD is a rectangle, if ∠BPC = 124°
Calculate:

1. ∠BAP
2. ∠ADP

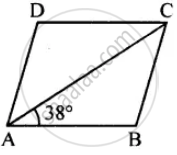
ABCD is a rhombus. If ∠BAC = 38°, find :
(i) ∠ACB
(ii) ∠DAC
(iii) ∠ADC.

ABCD is a rhombus. If ∠BCA = 35°. find ∠ADC.

PQRS is a parallelogram whose diagonals intersect at M.
If ∠PMS = 54°, ∠QSR = 25° and ∠SQR = 30° ; find :

(i) ∠RPS
(ii) ∠PRS
(iii) ∠PSR.

Given: Parallelogram ABCD in which diagonals AC and BD intersect at M.
Prove: M is the mid-point of LN.

In an Isosceles-trapezium, show that the opposite angles are supplementary.

ABCD is a parallelogram. What kind of quadrilateral is it if : AC = BD and AC is perpendicular to BD?

ABCD is a parallelogram. What kind of quadrilateral is it if: AC is perpendicular to BD but is not equal to it?

ABCD is a parallelogram. What kind of quadrilateral is it if: AC = BD but AC is not perpendicular to BD?

Prove that the diagonals of a parallelogram bisect each other.

If the diagonals of a parallelogram are of equal lengths, the parallelogram is a rectangle. Prove it.

In parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.

In parallelogram ABCD, E is the mid-point of side AB and CE bisects angle BCD. Prove that :

(i) AE = AD,
(ii) DE bisects and ∠ADC and
(iii) Angle DEC is a right angle.

In the following diagram, the bisectors of interior angles of the parallelogram PQRS enclose a quadrilateral ABCD.

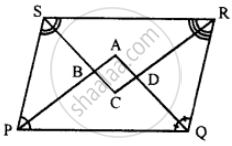
Show that:
(i) ∠PSB + ∠SPB = 90°
(ii) ∠PBS = 90°
(iii) ∠ABC = 90°
(iv) ∠ADC = 90°
(v) ∠A = 90°
(vi) ABCD is a rectangle
Thus, the bisectors of the angles of a parallelogram enclose a rectangle.

In parallelogram ABCD, X and Y are midpoints of opposite sides AB and DC respectively. Prove that:

(i) AX = YC
(ii) AX is parallel to YC
(iii) AXCY is a parallelogram.

The given figure shows parallelogram ABCD. Points M and N lie in diagonal BD such that DM = BN.

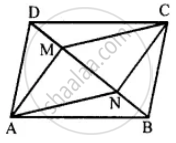
Prove that:
(i) ∆DMC = ∆BNA and so CM = AN
(ii) ∆AMD = ∆CNB and so AM CN
(iii) ANCM is a parallelogram.

The given figure shows a rhombus ABCD in which angle BCD = 80°. Find angles x and y.

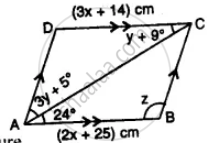
Use the information given in the alongside diagram to find the value of x, y, and z.

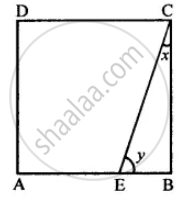
The following figure is a rectangle in which x: y = 3: 7; find the values of x and y.

In the given figure, AB || EC, AB = AC and AE bisects ∠DAC. Prove that:

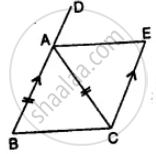
1. ∠EAC = ∠ACB
2. ABCE is a parallelogram.