Advertisements
Advertisements
प्रश्न
In parallelogram ABCD, ∠A = 3 times ∠B. Find all the angles of the parallelogram. In the same parallelogram, if AB = 5x – 7 and CD = 3x +1 ; find the length of CD.
उत्तर
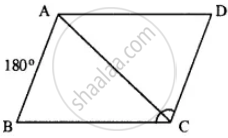
Let ∠B = x
∠A = 3 ∠B = 3x
AD || BC
∠A + ∠B = 180°
3x + x = 180°
⇒ 4x = 180°
⇒ x = 45°
∠B = 45°
∠A = 3x = 3 x 45 = 135°
and ∠B = ∠D = 45°
opposite angles of || gm are equal.
∠A = ∠C = 135°
opposite sides of //gm are equal.
AB = CD
5x – 7 = 3x + 1
⇒ 5x – 3x = 1+7
⇒ 2x = 8
⇒ x = 4
CD = 3 x 4+1 = 13
Hence 135°, 45°, 135° and 45° ; 13
APPEARS IN
संबंधित प्रश्न
Can a quadrilateral ABCD be a parallelogram if ∠A = 70° and ∠C = 65°?
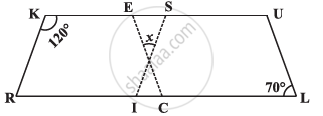
In the above figure both RISK and CLUE are parallelograms. Find the value of x.
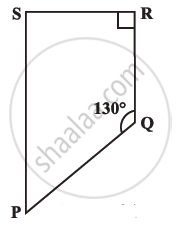
Find the measure of ∠P and ∠S, if `bar(SP) || bar(RQ)` in the following figure. (If you find m∠R, is there more than one method to find m∠P?).
Name the quadrilaterals whose diagonals bisect each other
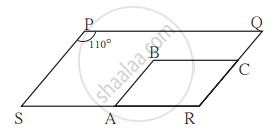
In the given figure, `square`PQRS and `square`ABCR are two parallelograms. If ∠P = 110° then find the measures of all angles of `square`ABCR.
Referring the adjacent figure of a parallelogram, write the answer of questions given below.
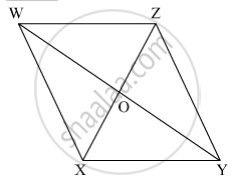
(1) If l(WZ) = 4.5 cm then l(XY) = ?
(2) If l(YZ) = 8.2 cm then l(XW) = ?
(3) If l(OX) = 2.5 cm then l(OZ) = ?
(4) If l(WO) = 3.3 cm then l(WY) = ?
(5) If m∠WZY = 120° then m∠WXY = ? and m∠XWZ = ?
In the following diagram, the bisectors of interior angles of the parallelogram PQRS enclose a quadrilateral ABCD.
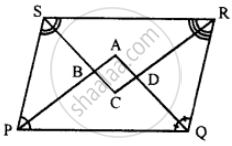
Show that:
(i) ∠PSB + ∠SPB = 90°
(ii) ∠PBS = 90°
(iii) ∠ABC = 90°
(iv) ∠ADC = 90°
(v) ∠A = 90°
(vi) ABCD is a rectangle
Thus, the bisectors of the angles of a parallelogram enclose a rectangle.
Use the information given in the alongside diagram to find the value of x, y, and z.
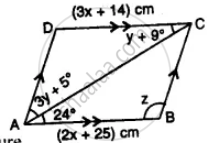
If two adjacent angles of a parallelogram are (5x – 5)° and (10x + 35)°, then the ratio of these angles is ______.
In parallelogram LOST, SN ⊥ OL and SM ⊥ LT. Find ∠STM, ∠SON and ∠NSM.

