Advertisements
Advertisements
प्रश्न
In parallelogram LOST, SN ⊥ OL and SM ⊥ LT. Find ∠STM, ∠SON and ∠NSM.

उत्तर
Given, ∠MST = 40°
In ΔMST,
By the angle sum property of a triangle,
∠TMS + ∠MST + ∠STM = 180°
⇒ ∠STM = 180° – (90° + 40°) ...[∵ SM ⊥ LT, ∠TMS = 90°]
= 50°
∴ ∠SON = ∠STM = 50° ...[∵ Opposite angles of a parallelogram are equal]
Now, In the ΔONS,
∠ONS + ∠OSN + ∠SON = 180° ...[Angle sum property of triangle]
∠OSN = 180° – (90° + 50°)
= 180° – 140°
= 40°
Moreover, ∠SON + ∠TSO = 180° ...[∵ Adjacent angles of a parallelogram are supplementary]
⇒ ∠SON + ∠TSM + ∠NSM + ∠OSN = 180°
⇒ 50° + 40° + ∠NSM + 40° = 180°
⇒ 90° + 40° + ∠NSM = 180°
⇒ 130° + ∠NSM = 180°
⇒ ∠NSM = 180° – 130° = 50°
APPEARS IN
संबंधित प्रश्न
The measures of two adjacent angles of a parallelogram are in the ratio 3 : 2. Find the measure of each of the angles of the parallelogram.
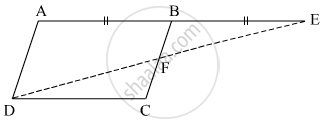
In the given figure, `square`ABCD is a parallelogram. Point E is on the ray AB such that BE = AB then prove that line ED bisects seg BC at point F.
Construct ☐ BARC such that l(BA) = l(BC) = 4.2 cm, l(AC) = 6.0 cm, l(AR) = l(CR) = 5.6 cm
In parallelogram ABCD, ∠A = 3 times ∠B. Find all the angles of the parallelogram. In the same parallelogram, if AB = 5x – 7 and CD = 3x +1 ; find the length of CD.
Prove that the diagonals of a parallelogram bisect each other.
In parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.
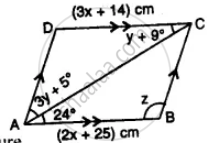
Use the information given in the alongside diagram to find the value of x, y, and z.
All rectangles are parallelograms.
If opposite angles of a quadrilateral are equal, it must be a parallelogram.
Construct a parallelogram when one of its side is 4 cm and its two diagonals are 5.6 cm and 7 cm. Measure the other side.
