Advertisements
Advertisements
Question
In parallelogram LOST, SN ⊥ OL and SM ⊥ LT. Find ∠STM, ∠SON and ∠NSM.

Solution
Given, ∠MST = 40°
In ΔMST,
By the angle sum property of a triangle,
∠TMS + ∠MST + ∠STM = 180°
⇒ ∠STM = 180° – (90° + 40°) ...[∵ SM ⊥ LT, ∠TMS = 90°]
= 50°
∴ ∠SON = ∠STM = 50° ...[∵ Opposite angles of a parallelogram are equal]
Now, In the ΔONS,
∠ONS + ∠OSN + ∠SON = 180° ...[Angle sum property of triangle]
∠OSN = 180° – (90° + 50°)
= 180° – 140°
= 40°
Moreover, ∠SON + ∠TSO = 180° ...[∵ Adjacent angles of a parallelogram are supplementary]
⇒ ∠SON + ∠TSM + ∠NSM + ∠OSN = 180°
⇒ 50° + 40° + ∠NSM + 40° = 180°
⇒ 90° + 40° + ∠NSM = 180°
⇒ 130° + ∠NSM = 180°
⇒ ∠NSM = 180° – 130° = 50°
APPEARS IN
RELATED QUESTIONS
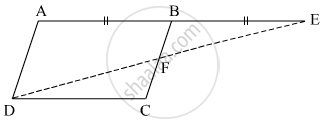
In the given figure, `square`ABCD is a parallelogram. Point E is on the ray AB such that BE = AB then prove that line ED bisects seg BC at point F.
In parallelogram PQRS, ∠Q = (4x – 5)° and ∠S = (3x + 10)°. Calculate: ∠Q and ∠R.
In parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.
In the following diagram, the bisectors of interior angles of the parallelogram PQRS enclose a quadrilateral ABCD.
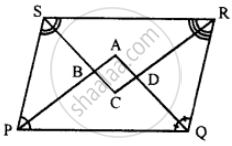
Show that:
(i) ∠PSB + ∠SPB = 90°
(ii) ∠PBS = 90°
(iii) ∠ABC = 90°
(iv) ∠ADC = 90°
(v) ∠A = 90°
(vi) ABCD is a rectangle
Thus, the bisectors of the angles of a parallelogram enclose a rectangle.
If a triangle and a parallelogram lie on the same base and between the same parallels, then prove that the area of the triangle is equal to half of the area of parallelogram
Iron rods a, b, c, d, e, and f are making a design in a bridge as shown in the figure. If a || b, c || d, e || f, find the marked angles between d and f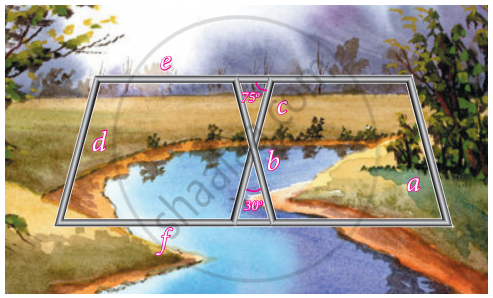
Which of the following figures satisfy the following properties?
- All sides are congruent.
- All angles are right angles.
- Opposite sides are parallel.
In parallelogram PQRS, O is the mid point of SQ. Find ∠S, ∠R, PQ, QR and diagonal PR.
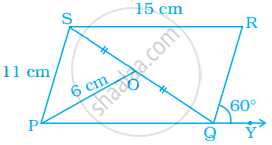
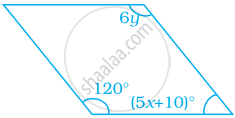
Find the values of x and y in the following parallelogram.
Construct a parallelogram HOME with HO = 6 cm, HE = 4 cm and OE = 3 cm.
