Advertisements
Chapters
2: Exponents
3: Squares and Square Root
4: Cubes and Cube Roots
5: Playing with Numbers
6: Sets
7: Percent and Percentage
8: Profit, Loss and Discount
9: Interest
10: Direct and Inverse Variations
11: Algebraic Expressions
12: Identities
13: Factorisation
14: Linear Equations in one Variable
15: Linear Inequations
▶ 16: Understanding Shapes
17: Special Types of Quadrilaterals
18: Constructions
19: Representing 3-D in 2-D
20: Area of a Trapezium and a Polygon
21: Surface Area, Volume and Capacity
22: Data Handling
23: Probability
![Selina solutions for Concise Mathematics [English] Class 8 ICSE chapter 16 - Understanding Shapes Selina solutions for Concise Mathematics [English] Class 8 ICSE chapter 16 - Understanding Shapes - Shaalaa.com](/images/concise-mathematics-english-class-8-icse_6:3b78c4422443458583dde48f228ef792.jpg)
Advertisements
Solutions for Chapter 16: Understanding Shapes
Below listed, you can find solutions for Chapter 16 of CISCE Selina for Concise Mathematics [English] Class 8 ICSE.
Selina solutions for Concise Mathematics [English] Class 8 ICSE 16 Understanding Shapes Exercise 16 (A) [Pages 180 - 181]
State which of the following are polygons :
(i)

(ii)

(iii)
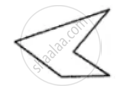
(iv)
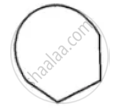
(v)
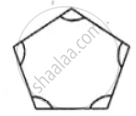
(vi)
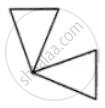
If the given figure is a polygon, name it as convex or concave.
Calculate the sum of angle of a polygon with: 10 sides
Calculate the sum of angle of a polygon with: 12 sides
Calculate the sum of angle of a polygon with: 20 sides
Calculate the sum of angle of a polygon with : 25 sides
Find the number of sides in a polygon if the sum of its interior angle is: 900°
Find the number of sides in a polygon if the sum of its interior angle is: 1620°
Find the number of sides in a polygon if the sum of its interior angle is: 16 right-angles.
Find the number of sides in a polygon if the sum of its interior angle is: 32 right-angles.
Is it possible to have a polygon, whose sum of interior angle is: 870°
Is it possible to have a polygon, whose sum of interior angle is: 2340°
Is it possible to have a polygon, whose sum of interior angle is: 7 right-angles
Is it possible to have a polygon, whose sum of interior angle is: 4500°
If all the angles of a hexagon are equal, find the measure of each angle.
If all the angles of a 14-sided figure are equal ; find the measure of each angle.
Find the sum of exterior angle obtained on producing, in order, the side of a polygon with: 7 sides
Find the sum of exterior angle obtained on producing, in order, the side of a polygon with : 10 sides
Find the sum of exterior angle obtained on producing, in order, the side of a polygon with: 250 sides
The sides of a hexagon are produced in order. If the measures of exterior angles so obtained are (6x – 1)°, (10x + 2)°, (8x + 2)° (9x – 3)°, (5x + 4)° and (12x + 6)° ; find each exterior angle.
The interior angles of a pentagon are in the ratio 4 : 5 : 6 : 7 : 5. Find each angle of the pentagon.
Two angles of a hexagon are 120° and 160°. If the remaining four angles are equal, find each equal angle.
The figure, given below, shows a pentagon ABCDE with sides AB and ED parallel to each other, and ∠B : ∠C : ∠D = 5: 6: 7.
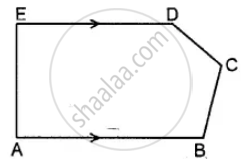
(i) Using the formula, find the sum of the interior angles of the pentagon.
(ii) Write the value of ∠A + ∠E
(iii) Find angles B, C and D.
Two angles of a polygon are right angles and the remaining are 120° each. Find the number of sides in it.
In a hexagon ABCDEF, side AB is parallel to side FE and ∠B : ∠C : ∠D : ∠E = 6 : 4 : 2 : 3. Find ∠B and ∠D.
The angles of a hexagon are x + 10°, 2x + 20°, 2x – 20°, 3x – 50°, x + 40° and x + 20°. Find x.
In a pentagon, two angles are 40° and 60°, and the rest are in the ratio 1 : 3 : 7. Find the biggest angle of the pentagon.
Selina solutions for Concise Mathematics [English] Class 8 ICSE 16 Understanding Shapes Exercise 16 (B) [Pages 184 - 185]
Fill in the blanks :
In case of regular polygon, with :
| No.of.sides | Each exterior angle | Each interior angle |
| (i) ___8___ | _______ | ______ |
| (ii) ___12____ | _______ | ______ |
| (iii) _________ | _____72°_____ | ______ |
| (iv) _________ | _____45°_____ | ______ |
| (v) _________ | __________ | _____150°_____ |
| (vi) ________ | __________ | ______140°____ |
Find the number of sides in a regular polygon, if its interior angle is: 160°
Find the number of sides in a regular polygon, if its interior angle is: 135°
Find the number of sides in a regular polygon, if its interior angle is: `1 1/5` of a right angle
Find the number of sides in a regular polygon, if its exterior angle is : `1/3` of right angle
Find the number of sides in a regular polygon, if its exterior angle is: two-fifth of right angle
Is it possible to have a regular polygon whose interior angle is : 170°
Is it possible to have a regular polygon whose interior angle is:
138°
Is it possible to have a regular polygon whose each exterior angle is: 80°
Is it possible to have a regular polygon whose each exterior angle is: 40° of a right angle.
Find the number of sides in a regular polygon, if its interior angle is equal to its exterior angle.
The exterior angle of a regular polygon is one-third of its interior angle. Find the number of sides in the polygon.
The measure of each interior angle of a regular polygon is five times the measure of its exterior angle. Find :
(i) measure of each interior angle ;
(ii) measure of each exterior angle and
(iii) number of sides in the polygon.
The ratio between the interior angle and the exterior angle of a regular polygon is 2: 1. Find:
(i) each exterior angle of the polygon ;
(ii) number of sides in the polygon.
The ratio between the exterior angle and the interior angle of a regular polygon is 1 : 4. Find the number of sides in the polygon.
The sum of interior angles of a regular polygon is twice the sum of its exterior angles. Find the number of sides of the polygon.
AB, BC and CD are three consecutive sides of a regular polygon. If angle BAC = 20° ; find :
(i) its each interior angle,
(ii) its each exterior angle
(iii) the number of sides in the polygon.
Two alternate sides of a regular polygon, when produced, meet at the right angle. Calculate the number of sides in the polygon.
In a regular pentagon ABCDE, draw a diagonal BE and then find the measure of:
(i) ∠BAE
(ii) ∠ABE
(iii) ∠BED
The difference between the exterior angles of two regular polygons, having the sides equal to (n – 1) and (n + 1) is 9°. Find the value of n.
If the difference between the exterior angle of a 'n' sided regular polygon and an (n + 1) sided regular polygon is 12°, find the value of n.
The ratio between the number of sides of two regular polygons is 3 : 4 and the ratio between the sum of their interior angles is 2 : 3. Find the number of sides in each polygon.
Three of the exterior angles of a hexagon are 40°, 51 ° and 86°. If each of the remaining exterior angles is x°, find the value of x.
Calculate the number of sides of a regular polygon, if: its interior angle is five times its exterior angle.
Calculate the number of sides of a regular polygon, if: the ratio between its exterior angle and interior angle is 2: 7.
Calculate the number of sides of a regular polygon, if: its exterior angle exceeds its interior angle by 60°.
The sum of interior angles of a regular polygon is thrice the sum of its exterior angles. Find the number of sides in the polygon.
Selina solutions for Concise Mathematics [English] Class 8 ICSE 16 Understanding Shapes Exercise 16 (C) [Pages 187 - 188]
Two angles of a quadrilateral are 89° and 113°. If the other two angles are equal; find the equal angles.
Two angles of a quadrilateral are 68° and 76°. If the other two angles are in the ratio 5 : 7; find the measure of each of them.
Angles of a quadrilateral are (4x)°, 5(x+2)°, (7x – 20)° and 6(x+3)°. Find :
(i) the value of x.
(ii) each angle of the quadrilateral.
Use the information given in the following figure to find :
(i) x
(ii) ∠B and ∠C
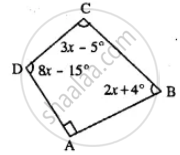
In quadrilateral ABCD, side AB is parallel to side DC. If ∠A : ∠D = 1 : 2 and ∠C : ∠B = 4 : 5
(i) Calculate each angle of the quadrilateral.
(ii) Assign a special name to quadrilateral ABCD
From the following figure find;
- x
- ∠ABC
- ∠ACD
Given : In quadrilateral ABCD ; ∠C = 64°, ∠D = ∠C – 8° ; ∠A = 5(a+2)° and ∠B = 2(2a+7)°.
Calculate ∠A.
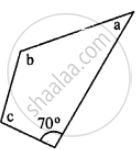
In the given figure : ∠b = 2a + 15 and ∠c = 3a + 5; find the values of b and c.
Three angles of a quadrilateral are equal. If the fourth angle is 69°; find the measure of equal angles.
In quadrilateral PQRS, ∠P : ∠Q : ∠R : ∠S = 3 : 4 : 6 : 7.
Calculate each angle of the quadrilateral and then prove that PQ and SR are parallel to each other
(i) Is PS also parallel to QR?
(ii) Assign a special name to quadrilateral PQRS.
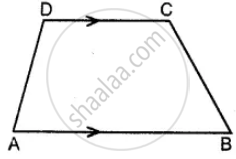
Use the information given in the following figure to find the value of x.
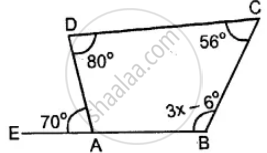
The following figure shows a quadrilateral in which sides AB and DC are parallel. If ∠A : ∠D = 4 : 5, ∠B = (3x – 15)° and ∠C = (4x + 20)°, find each angle of the quadrilateral ABCD.
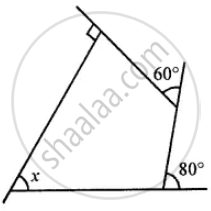
Use the following figure to find the value of x
ABCDE is a regular pentagon. The bisector of angle A of the pentagon meets the side CD in point M. Show that ∠AMC = 90°.
In a quadrilateral ABCD, AO and BO are bisectors of angle A and angle B respectively. Show that:
∠AOB = (∠C + ∠D)
Solutions for 16: Understanding Shapes
![Selina solutions for Concise Mathematics [English] Class 8 ICSE chapter 16 - Understanding Shapes Selina solutions for Concise Mathematics [English] Class 8 ICSE chapter 16 - Understanding Shapes - Shaalaa.com](/images/concise-mathematics-english-class-8-icse_6:3b78c4422443458583dde48f228ef792.jpg)
Selina solutions for Concise Mathematics [English] Class 8 ICSE chapter 16 - Understanding Shapes
Shaalaa.com has the CISCE Mathematics Concise Mathematics [English] Class 8 ICSE CISCE solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. Selina solutions for Mathematics Concise Mathematics [English] Class 8 ICSE CISCE 16 (Understanding Shapes) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. Selina textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Concise Mathematics [English] Class 8 ICSE chapter 16 Understanding Shapes are Different Types of Curves - Closed Curve, Open Curve, Simple Curve., Concept of Polygons, Sum of Angles of a Polynomial, Sum of Exterior Angles of a Polynomial, Regular Polynomial, Concept of Quadrilaterals.
Using Selina Concise Mathematics [English] Class 8 ICSE solutions Understanding Shapes exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in Selina Solutions are essential questions that can be asked in the final exam. Maximum CISCE Concise Mathematics [English] Class 8 ICSE students prefer Selina Textbook Solutions to score more in exams.
Get the free view of Chapter 16, Understanding Shapes Concise Mathematics [English] Class 8 ICSE additional questions for Mathematics Concise Mathematics [English] Class 8 ICSE CISCE, and you can use Shaalaa.com to keep it handy for your exam preparation.
