Advertisements
Advertisements
प्रश्न
ABCDE is a regular pentagon. The bisector of angle A of the pentagon meets the side CD in point M. Show that ∠AMC = 90°.
उत्तर
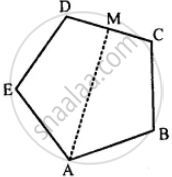
Given: ABCDE is a regular pentagon.
The bisector ∠A of the pentagon meets the side CD at point M.
To prove : ∠AMC = 90°
Proof: We know that the measure of each interior angle of a regular pentagon is 108°.
∠BAM = x 108° = 54°
Since, we know that the sum of a quadrilateral is 360°
In quadrilateral ABCM, we have
∠BAM + ∠ABC + ∠BCM + ∠AMC = 360°
54° + 108° + 108° + ∠AMC = 360°
∠AMC = 360° – 270°
∠AMC = 90°
APPEARS IN
संबंधित प्रश्न
The sides of a quadrilateral are produced in order. What is the sum of the four exterior angles?
Complete the following statement by means of one of those given in brackets against each:
A line drawn from the mid-point of one side of a triangle .............. another side intersects the third side at its mid-point.
In a quadrilateral ABCD, AO and BO are bisectors of angle A and angle B respectively. Show that:
∠AOB = (∠C + ∠D)
In an isosceles trapezium one pair of opposite sides are _____ to each Other and the other pair of opposite sides are _____ to each other.
The angles A, B, C and D of a quadrilateral are in the ratio 2 : 3 : 2 : 3. Show this quadrilateral is a parallelogram.
ΔPQR and ΔSQR are on the same base QR with P and S on opposite sides of line QR, such that area of ΔPQR is equal to the area of ΔSQR. Show that QR bisects PS.
ABCD is a rhombus such that ∠ACB = 40º. Then ∠ADB is ______.
If the sum of two angles is equal to an obtuse angle, then which of the following is not possible?
In the given figure.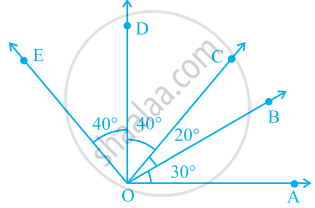
∠COA is a/an ______ angle
Draw a rough sketch of a quadrilateral KLMN. State two pairs of adjacent angles.
