Advertisements
Advertisements
प्रश्न
ABCDE is a regular pentagon. The bisector of angle A of the pentagon meets the side CD in point M. Show that ∠AMC = 90°.
उत्तर
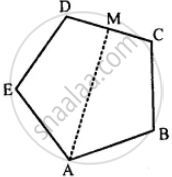
Given: ABCDE is a regular pentagon.
The bisector ∠A of the pentagon meets the side CD at point M.
To prove : ∠AMC = 90°
Proof: We know that the measure of each interior angle of a regular pentagon is 108°.
∠BAM = x 108° = 54°
Since, we know that the sum of a quadrilateral is 360°
In quadrilateral ABCM, we have
∠BAM + ∠ABC + ∠BCM + ∠AMC = 360°
54° + 108° + 108° + ∠AMC = 360°
∠AMC = 360° – 270°
∠AMC = 90°
APPEARS IN
संबंधित प्रश्न
Complete of the following, so as to make a true statement:
A quadrilateral has ...... angles.
Complete of the following, so as to make a true statement:
The number of pairs of adjacent angles of a quadrilateral is .......
Determine the number of sides of a polygon whose exterior and interior angles are in the ratio 1 : 5.
ABCD is a trapezium in which AB || DC. M and N are the mid-points of AD and the respectively. If AB = 12 cm, MN = 14 cm, then CD =
In a quadrilateral ABCD, AO and BO are bisectors of angle A and angle B respectively. Show that:
∠AOB = (∠C + ∠D)
In a pentagon ABCDE, AB || ED and ∠B = 140°, ∠C = 2x° and ∠D = 3x°. Find ∠C and ∠D
A diagonal of a rectangle is inclined to one side of the rectangle at 25º. The acute angle between the diagonals is ______.
In figure, if point A is shifted to point B along the ray PX such that PB = 2PA, then the measure of ∠BPY is ______.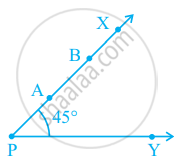
Using the information given, name the right angles in part of figure:
OP ⊥ AB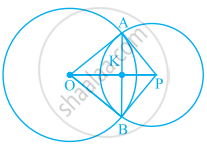
Can we have two obtuse angles whose sum is a complete angle? Why or why not?
