Question

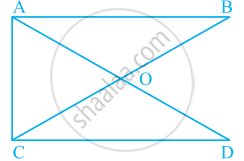
In a quadrilateral ABCD, AO and BO are bisectors of angle A and angle B respectively. Show that:

∠AOB = (∠C + ∠D)

Answer 1

In a quadrilateral ABCD, AO and BO are the bisectors of ∠A and ∠B, respectively. We need to prove that:

∠AOB = ∠C + ∠D.

The sum of the interior angles of a quadrilateral is: ∠A + ∠B + ∠C + ∠D = 360∘.

Since AO and BO are the bisectors of ∠A\ and ∠B\, we can express: `angleAOB=(angleA)/2+(angleB)/2`

From the sum of the interior angles of the quadrilateral, rearrange to find ∠A+∠B

∠A + ∠B = 360∘ − (∠C + ∠D).

Now substitute ∠A+∠B into the expression for ∠AOB:

`angleAOB= (angleA)/2+(angleB)/2=(angleA+angleB)/2`

Replace ∠A + ∠B with 360^∘ − (∠C + ∠D)

`angleAOB=(360°-(angleC+angleD))/2`

Simplify: `angleAOB = 180°-(angleC+angleD)/2`

∠AOB = ∠C + ∠D.