Advertisements
Advertisements
Question
In a quadrilateral ABCD, AO and BO are bisectors of angle A and angle B respectively. Show that:
∠AOB = (∠C + ∠D)
Solution
In a quadrilateral ABCD, AO and BO are the bisectors of ∠A and ∠B, respectively. We need to prove that:
∠AOB = ∠C + ∠D.
The sum of the interior angles of a quadrilateral is: ∠A + ∠B + ∠C + ∠D = 360∘.
Since AO and BO are the bisectors of ∠A\ and ∠B\, we can express: `angleAOB=(angleA)/2+(angleB)/2`
From the sum of the interior angles of the quadrilateral, rearrange to find ∠A+∠B
∠A + ∠B = 360∘ − (∠C + ∠D).
Now substitute ∠A+∠B into the expression for ∠AOB:
`angleAOB= (angleA)/2+(angleB)/2=(angleA+angleB)/2`
Replace ∠A + ∠B with 360∘ − (∠C + ∠D)
`angleAOB=(360°-(angleC+angleD))/2`
Simplify: `angleAOB = 180°-(angleC+angleD)/2`
∠AOB = ∠C + ∠D.
APPEARS IN
RELATED QUESTIONS
Complete of the following, so as to make a true statement:
A quadrilateral has ....... sides.
In Fig. 16.19, ABCD is a quadrilateral.
Name a pair of opposite angles.

Two angles of a quadrilateral are of measure 65° and the other two angles are equal. What is the measure of each of these two angles?
Mark the correct alternative in each of the following:
The opposite sides of a quadrilateral have
Observe the figure below and find out their name.
The three angles of a quadrilateral are 71°, 110°, 95°. Find its fourth angle.
ΔPQR and ΔSQR are on the same base QR with P and S on opposite sides of line QR, such that area of ΔPQR is equal to the area of ΔSQR. Show that QR bisects PS.
In a quadrilateral ABCD, ∠A = 72° and ∠C is the supplementary of ∠A. The other two angles are 2x – 10 and x + 4. Find the value of x and the measure of all the angles
Number of angles less than 180° in figure is ______ and their names are ______.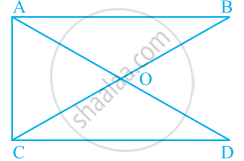
Draw a rough sketch of a quadrilateral KLMN. State two pairs of adjacent angles.
