Advertisements
Advertisements
Question
Two angles of a quadrilateral are of measure 65° and the other two angles are equal. What is the measure of each of these two angles?
Solution
\[ \text{ Let x be the measure of each angle } . \]
\[\text{ Since, the sum of all the angles of a quadrilateral is } 360 °, \text{ we have: } \]
\[65° + 65° + x° + x° = 360° \]
\[ \Rightarrow 2x° + 130°= 360° \]
\[ \Rightarrow 2x° = 230° \]
\[ \Rightarrow x° = 115°\]
\[ \therefore \text{ The measure of each angle is } 115° .\]
APPEARS IN
RELATED QUESTIONS
Complete the following statement by means of one of those given in brackets against each:
A line drawn from the mid-point of one side of a triangle .............. another side intersects the third side at its mid-point.
Two angles of a quadrilateral are 68° and 76°. If the other two angles are in the ratio 5 : 7; find the measure of each of them.
The following figure shows a quadrilateral in which sides AB and DC are parallel. If ∠A : ∠D = 4 : 5, ∠B = (3x – 15)° and ∠C = (4x + 20)°, find each angle of the quadrilateral ABCD.
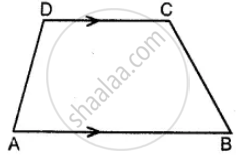
Angle A of an isosceles trapezium ABCD is 115°; find the angles B, C and D.
Observe the figure below and find out their name.
If angles A, B, C and D of the quadrilateral ABCD, taken in order, are in the ratio 3 : 7 : 6 : 4, then ABCD is a ______.
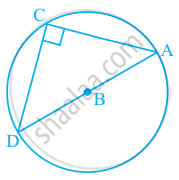
In the given figure.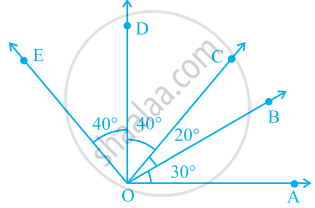
∠AOD is a/an ____ angle
The number of straight angles in figure is ______.
In given figure, name any four angles that appear to be acute angles.
Using the information given, name the right angles in part of figure:
AC ⊥ CD