Topics
Number Systems
Number Systems
Polynomials
Algebra
Coordinate Geometry
Linear Equations in Two Variables
Geometry
Coordinate Geometry
Introduction to Euclid’S Geometry
Mensuration
Statistics and Probability
Lines and Angles
- Introduction to Lines and Angles
- Basic Terms and Definitions
- Intersecting Lines and Non-intersecting Lines
- Introduction to Parallel Lines
- Pairs of Angles
- Parallel Lines and a Transversal
- Angle Sum Property of a Triangle
Triangles
- Concept of Triangles
- Congruence of Triangles
- Criteria for Congruence of Triangles
- Properties of a Triangle
- Some More Criteria for Congruence of Triangles
- Inequalities in a Triangle
Quadrilaterals
- Concept of Quadrilaterals
- Properties of a Quadrilateral
- Types of Quadrilaterals
- Another Condition for a Quadrilateral to Be a Parallelogram
- Theorem of Midpoints of Two Sides of a Triangle
- Property: The Opposite Sides of a Parallelogram Are of Equal Length.
- Theorem: A Diagonal of a Parallelogram Divides It into Two Congruent Triangles.
- Theorem : If Each Pair of Opposite Sides of a Quadrilateral is Equal, Then It is a Parallelogram.
- Property: The Opposite Angles of a Parallelogram Are of Equal Measure.
- Theorem: If in a Quadrilateral, Each Pair of Opposite Angles is Equal, Then It is a Parallelogram.
- Property: The diagonals of a parallelogram bisect each other. (at the point of their intersection)
- Theorem : If the Diagonals of a Quadrilateral Bisect Each Other, Then It is a Parallelogram
Circles
Areas - Heron’S Formula
Surface Areas and Volumes
Statistics
Algebraic Expressions
Algebraic Identities
Area
Constructions
- Introduction of Constructions
- Basic Constructions
- Some Constructions of Triangles
Probability
- Introduction:
- Reading and Writing of a Quadrilateral
Definition
Quadrilaterals: A four-sided polygon is a quadrilateral. Any four points in a plane, out of which three are non-collinear are joined in order to formed a four-sided closed figure called ‘quadrilateral’.
Notes
Quadrilaterals:
- Any four points in a plane, out of which three are non-collinear are joined in order to formed a four-sided closed figure called ‘quadrilateral’.
- A quadrilateral has four sides, four angles and four vertices. Quadrilateral could be regular or irregular.
-
A four-sided polygon is a quadrilateral.
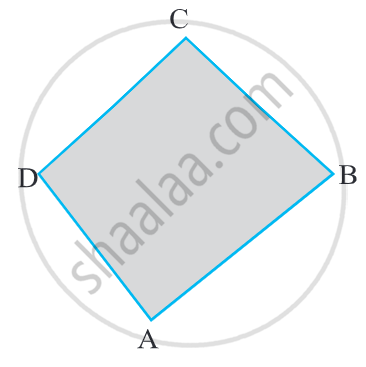
- Quadrilateral ABCD has four sides `bar"AB", bar"BC", bar"CD", and bar"DA"`.
- It has four angles ∠A, ∠B, ∠C, and ∠D.
- A, B, C and D are the four vertices and
- BD and AC are the two diagonals of the quadrilateral ABCD.
Reading and Writing of a Quadrilateral:
-
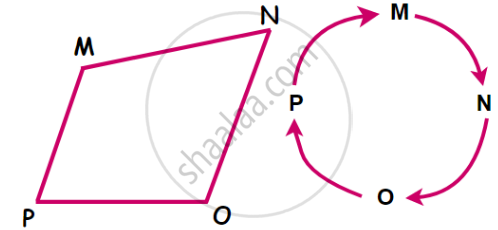
A quadrilateral can be named by starting at any vertex and going serially either clockwise or anti-clockwise around the figure.
-
When writing the name of a quadrilateral a sign like this ‘□’ is put in place of the word ‘quadrilateral’.
A quadrilateral can be named by starting at any vertex and going serially either clockwise or anti-clockwise around the figure.
When writing the name of a quadrilateral a sign like this ‘□’ is put in place of the word ‘quadrilateral’.
| Clockwise | Anti-clockwise | ||
| Reading | Writing | Reading | Writing |
| Quadrilateral MNOP | □ MNOP | Quadrilateral PONM | □ PONM |
| Quadrilateral NOPM | □ NOPM | Quadrilateral ONMP | □ ONMP |
| Quadrilateral OPMN | □ OPMN | Quadrilateral NMPO | □ NMPO |
| Quadrilateral PMNO | □ PMNO | Quadrilateral MPON | □ MPON |
1. Adjacent Sides of a Quadrilateral:

- Adjacent sides of the quadrilateral have a common vertex.
- The sides MN and MP of □ MNOP have a common vertex M. Sides MN and MP are adjacent sides.
- Every quadrilateral has four pairs of adjacent sides.
Pairs of adjacent sides:
-
Side MN and Side MP
-
Side MN and Side NO
-
Side NO and Side OP
-
Side OP and Side MP.
2. Opposite Sides of a Quadrilateral:
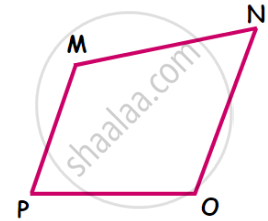
- Opposite sides of the quadrilateral do not have a common vertex.
- In □ MNOP the sides MP and NO have no common vertex.
- Side MP and side NO are opposite sides of the quadrilateral.
Pairs of opposite sides:
-
sides MP and NO
-
sides MN and PO
3. Adjacent Angles of a Quadrilateral:

- The angles of a quadrilateral which have one common arm are called adjacent angles of the quadrilateral.
- These angles are neighbouring or adjacent angles.
Name the adjacent angles of the quadrilateral MNOP.
-
∠MNO and ∠PMN
-
∠MPO and ∠NOP
-
∠PON and ∠MNO
-
∠ONM and ∠PMN
4. Opposite Angles of a Quadrilateral:

- The angles of a quadrilateral which do not have a common arm are called opposite angles of a quadrilateral.
- They lie opposite to each other.
Pair of Opposite angle:
- Angle opposite to ∠PMN is ∠NOP.
- Angle opposite to ∠MNO is ∠OPM.
5. Diagonals of a Quadrilateral:
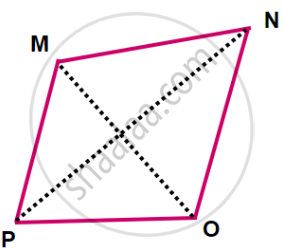
- The line segments which join the vertices of the opposite angles of a quadrilateral are the diagonals of the quadrilateral.
- The segments MO and NP are the diagonals of the quadrilateral ABCD.
6. Interior & Exterior of A Quadrilateral:
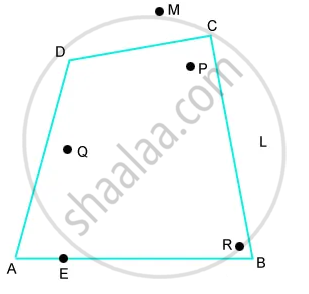
- Being a polygon, a quadrilateral has an exterior and an interior.
- P, Q, and R are in the interior of the quadrilateral, M and L are in the exterior, and A, B, C, D, and E on the quadrilateral.
If you would like to contribute notes or other learning material, please submit them using the button below.
Shaalaa.com | Quadrilateral
to track your progress