Advertisements
Advertisements
Question
If bisectors of ∠A and ∠B of a quadrilateral ABCD intersect each other at P, of ∠B and ∠C at Q, of ∠C and ∠D at R and of ∠D and ∠A at S, then PQRS is a ______.
Options
rectangle
rhombus
parallelogram
quadrilateral whose opposite angles are supplementary
Solution
If bisectors of ∠A and ∠B of a quadrilateral ABCD intersect each other at P, of ∠B and ∠C at Q, of ∠C and ∠D at R and of ∠D and ∠A at S, then PQRS is a quadrilateral whose opposite angles are supplementary
Explanation:
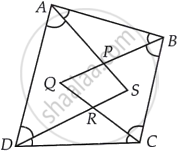
Sum of all angles of a quadrilateral is 360°
⇒ ∠A + ∠B + ∠C + ∠D = 360°
On dividing both sides by 2,
⇒ `1/2` (∠A + ∠B + ∠C + ∠D) = `1/2` × 360° = 180°
∵ AP, PB, RC and RD are bisectors of ∠A, ∠B, ∠C and ∠D
⇒ ∠PAB + ∠ABB + ∠RCD + ∠RDC = 180° ...(1)
Sum of all angles of a triangle is 180°
∴ ∠PAB + ∠APB + ∠ABP = 180°
⇒ ∠PAB + ∠ABP = 180° – ∠APB ...(2)
Similarly,
∴ ∠RDC + ∠RCD + ∠CRD = 180°
⇒ ∠RDC + ∠RCD = 180° – ∠CRD ...(3)
Putting (2) and (3) in (1),
180° – ∠APB + 180° – ∠CRD = 180°
⇒ 360° – ∠APB – ∠CRD = 180°
⇒ ∠APB + ∠CRD = 360° – 180°
⇒ ∠APB + ∠CRD = 180° ...(4)
Now,
∠SPQ = ∠APB ...[Vertically opposite angles]
∠SRQ = ∠DRC ...[Vertically opposite angles]
Putting in (4),
⇒ ∠SPQ + ∠SRQ = 180°
APPEARS IN
RELATED QUESTIONS
In a quadrilateral, define of the following Angles .
Complete of the following, so as to make a true statement:
A quadrilateral has ...... angles.
In Fig. 16.19, ABCD is a quadrilateral.
How many pairs of adjacent angles are there?
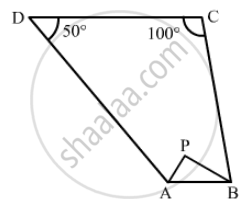
In Fig. 16.21, the bisectors of ∠A and ∠B meet at a point P. If ∠C = 100° and ∠D = 50°, find the measure of ∠APB.
In the given figure : ∠b = 2a + 15 and ∠c = 3a + 5; find the values of b and c.
ABCDE is a regular pentagon. The bisector of angle A of the pentagon meets the side CD in point M. Show that ∠AMC = 90°.
The angles A, B, C and D of a quadrilateral are in the ratio 2 : 3 : 2 : 3. Show this quadrilateral is a parallelogram.
Find the angles of a pentagon which are in the ratio 4: 4: 6: 7: 6.
The number of right angles in a straight angle is ______ and that in a complete angle is ______.
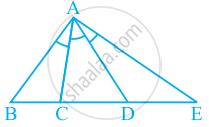
An angle is said to be trisected, if it is divided into three equal parts. If in the given figure, ∠BAC = ∠CAD = ∠DAE, how many trisectors are there for ∠BAE?