Advertisements
Advertisements
Question
In Fig. 16.21, the bisectors of ∠A and ∠B meet at a point P. If ∠C = 100° and ∠D = 50°, find the measure of ∠APB.
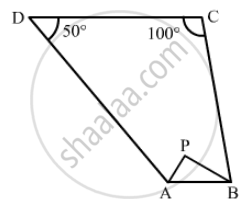
Solution
\[∠A + ∠B + ∠C +∠D = 360° \]
\[ \Rightarrow ∠A +∠B + 100°+ 50° = 360° \]
\[ \Rightarrow ∠A + ∠B = 210° . . . (i)\]
\[\text{ In } \bigtriangleup APB, \text{ we have } : \]
\[\frac{1}{2}∠A + \frac{1}{2}∠B + ∠APB = 180° \]
\[ \Rightarrow ∠APB = 180° - \frac{1}{2}\left( ∠A + ∠B \right)\]
\[\text{ From (i), we get: } \]
\[ \Rightarrow ∠APB = 180° - \left( \frac{1}{2} \times 210° \right) \]
\[ \therefore ∠APB = 75° \]
APPEARS IN
RELATED QUESTIONS
In a quadrilateral, define of the following Interior .
In the given figure, ABCD is a trapezium. Find the values of x and y.

Complete the following statement by means of one of those given in brackets against each:
If opposite angles of a quadrilateral are equal, then it is necessarily a ....................
Two adjacent angles of a parallelogram are 70° and 110° respectively. Find the other two angles of it.
One diagonal of a rectangle is 18 cm. What is the length of its other diagonal?
In the figure, PQRS and PTVS are two cyclic quadrilaterals, If ∠QRS = 100°, then ∠TVS =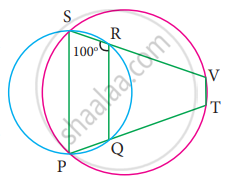
ABCD is a quadrilateral in which AB || DC and AD = BC. Prove that ∠A = ∠B and ∠C = ∠D.
A pair of opposite sides of a trapezium are ______.
The number of straight angles in figure is ______.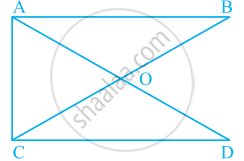
Draw a rough sketch of a quadrilateral PQRS. Draw its diagonals. Name them. Is the meeting point of the diagonals in the interior or exterior of the quadrilateral?